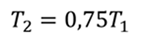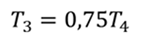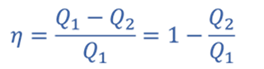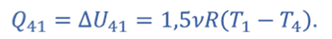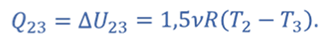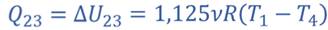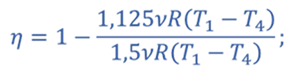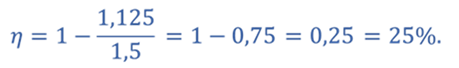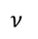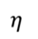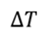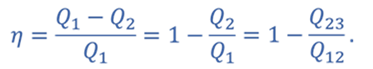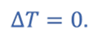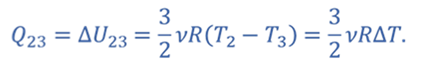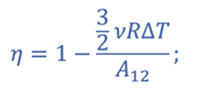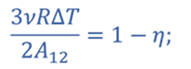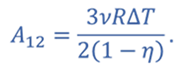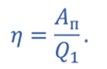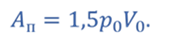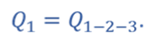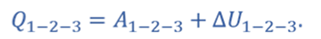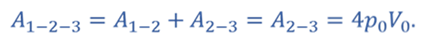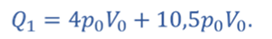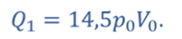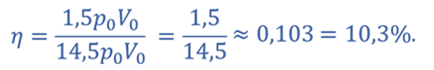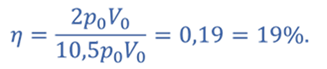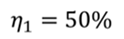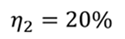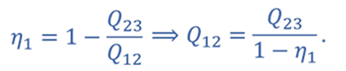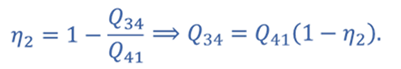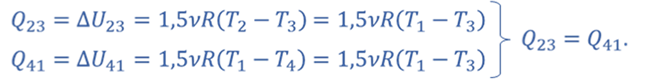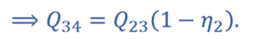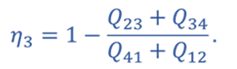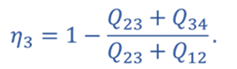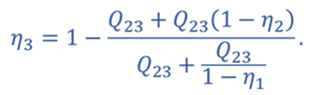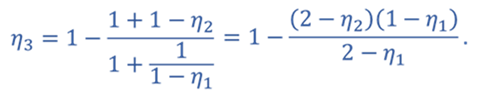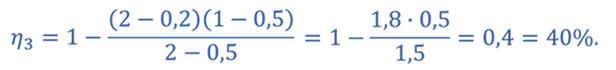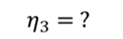Тепловые машины. КПД

Образовательные цели урока: повторение графиков изопроцессов, закрепление умений чтения графиков изопроцессов и решения задач на первый закон термодинамики, формирование умений определять КПД тепловой машины по графику и общеучебных навыков (работы с текстом, выделения главного, преобразования информации из одного вида в другой).

Методы: эвристическая беседа, самостоятельная работа, дифференциация.

Оборудование: распечатанные для каждого ученика условие задачи и решение (вариант А), распечатанные на каждую парту условия задач различного уровня сложности для самостоятельной работы. (Возможно использование интерактивной доски.)

Ход урока

1. Организационный этап

2. Индуктор. На доске написан вариант А решения задачи. Учитель утверждает, что с таким сложным решением трудно разобраться, его невозможно запомнить. Что же делать? Для облегчения работы каждому ученику выдаётся вариант B решения задачи – копия А, но с пропусками.

3. Осмысление. Учащиеся предлагают разбить решение на логически завершённые части. Учитель обращает их внимание на сложные места в решении, причём не даёт объяснение, а только спрашивает: для чего эта запись? почему записано именно так? В результате работы текст решения превращается из первоначального варианта А в вариант с дополнениями В.

Задача

• Тепловая машина, рабочим телом которой является идеальный одноатомный газ, работает по циклу 1–2–3–1. Найдите КПД этой машины.

Исходный вариант решения (А, записан на доске).

Вариант решения B с дополнениями, написанными учениками в своих экземплярах и на доске в ходе урока. (Дополнения выделены другим шрифтом и цветом. Условие здесь не повторено. – Ред.)

Учитель предлагает применить полученные знания для решения подобной задачи или повторить решение этой же задачи. Каждый ученик выбирает для себя способ подсказки: глядя только на часть решённой задачи, восстановить всё решение; никуда не глядя, восстановить всё решение; глядя в решение, решить новую подобную задачу; решить задачу повышенного уровня сложности. Ученики выполняют самостоятельную работу.

Задачи для самостоятельного решения

• 1 моль идеального одноатомного газа совершает цикл, изображённый на рисунке, в координатах p, U, где p – давление, U – внутренняя энергия газа. Определите КПД цикла. (Ответ. КПД = 2/13 ≈ 15%.)

• Докажите, что КПД тепловой машины, работающей по циклу из двух изотерм и двух изохор, меньше КПД идеальной тепловой машины, работающей по циклу Карно, с тем же нагревателем и холодильником.

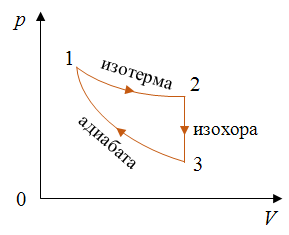
• КПД тепловой машины, работающей по циклу, состоящему из изотермы 1–2, изохоры 2–3, адиабаты 3–1, равен η, разность между максимальной и минимальной температурами газа в цикле равна ∆T. Найдите работу, совершённую ν молями одноатомного идеального газа в изотермическом процессе. (Ответ. )

• Найдите КПД тепловой машины, работающей по циклам 1–2–3–1; 1–3–4–1. рабочим телом является одноатомный идеальный газ. (Ответ. КПД = 2/23 ≈ 8,7%; КПД = 2/21 ≈ 9,5%.)

• Найдите КПД тепловой машины, работающей по циклам 1–2–3–4–1. рабочим телом является молекулярный водород. (Ответ. КПД = 6/43 ≈ 14%.)

4. Рефлексия. Школьники пишут эссе – своё мнение о значении проверки в решении задачи. Желающие зачитывают вслух.

5. ДЗ. Напишите алгоритм решения задачи и свои рекомендации своим отсутствовавшим товарищам.

Тепловые машины и второе начало термодинамики

теория по физике 🧲 термодинамика

Тепловые машины — устройства, в которых за счет внутренней энергии топлива совершается механическая работа. Чтобы тепловая машина работала циклически, необходимо, чтобы часть энергии, полученной от нагревателя, она отдавала холодильнику.

Второе начало термодинамики

В циклически действующем тепловом двигателе невозможно преобразовать все количество теплоты, полученное от нагревателя, в механическую работу.

В тепловых машинах тепловые процессы замыкаются в цикле Карно. Так называют цикл, или идеальный круговой процесс, состоящий из двух адиабатных и двух изотермических процессов. В цикле Карно термодинамическая система выполняет механическую работу за счет обмена теплотой с двумя тепловыми резервуарами, имеющими постоянные, но различающиеся температуры.

На графике цикл Карно представляется как две адиабаты и две изотермы:

• 1–2 — изотермическое расширение;
• 2–3 — адиабатное расширение;
• 3–4 — изотермическое сжатие;
• 4–1 — адиабатное сжатие.

КПД тепловой машины

Максимальный КПД соответствует циклу Карно.

Второе начало термодинамики

η = Q н − Q х Q н . . 100 % = Q н − P х t Q н . . 100 %

Преобразовывая формулу, получим:

η = A ‘ Q н . . 100 %

η = N t Q н . . 100 %

η = A ‘ A ‘ + Q х . . 100 %

η = T н − T х T н . . 100 %

1. Q_н (Дж) — количество теплоты, полученное от нагревателя (полученное количество теплоты);
2. Q_х (Дж) — количество теплоты, отданное холодильнику (отданное количество теплоты);
3. A’ (Дж) — работа, совершенная газом;
4. N (Вт) — полезная мощность;
5. t (с) — время;
6. T_н (К) — температура нагревателя;
7. T_х (К) — температура холодильника.

Важно! Температуру следует выражать только в кельвинах (К) и КПД не бывает больше 100%.

Алгоритм решения задач на определение КПД теплового процесса

Рассмотрим решение на примере конкретной задачи:

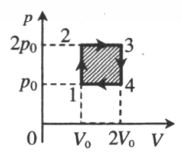
На p-V-диаграмме изображен цикл, проводимый с одноатомным идеальным газом. Определите КПД этого цикла.

Если тепловой процесс представлен в осях (p, V), то можно определить работу, вычислив площадь фигуры, ограниченной замкнутым циклом:

Если тепловой процесс представлен в других осях координат, то сначала следует его перестроить в осях (p, V) и только потом определять работу.

• Выяснить, на каких этапах повышается температура газа. Именно здесь газ получает энергию:

1–2: V = const, давление увеличивается, температура увеличивается.

2–3: p = const, объем увеличивается, температура увеличивается.

3–4: V = const, давление понижается, температура понижается.

4–1: p = const, объем уменьшается, температура уменьшается.

Отсюда следует, что газ получает энергию только на первом и втором этапах.

• Определить с помощью первого начала термодинамики количество теплоты, полученное газом:

Q 12 = Δ U 12 = 3 2 . . Δ p V = 3 2 . . Δ p 0 V 0 = 1 , 5 p 0 V 0

Δ U 23 = Q 23 − A 23 ;

Δ U 23 = 3 2 . . Δ p V = 3 2 . . 2 Δ p 0 V 0 = 3 p 0 V 0

A 23 = p Δ V = 2 p 0 V 0

Q 23 = 3 p 0 V 0 + 2 p 0 V 0 = 5 p 0 V 0

Общее количество теплоты:

Q п о л у ч = Q 12 + Q 23 = 6 , 5 p 0 V 0

• Вычислить КПД, используя основную формулу:

η = A ‘ Q п о л у ч . . 100 %

η = p 0 V 0 6 , 5 p 0 V 0 . . 100 % = 15 , 4 %

За цикл, показанный на рисунке, газ получает от нагревателя количество теплоты Q_нагр = 5,1кДж. КПД цикла равен 4/17. Масса газа постоянна. На участке 1–2 газ совершает работу

Тепловые двигатели. Коэффициент полезного действия теплового двигателя (продолжение)

Урок 12. Решение задач по основам МКТ, оптике и квантовой физике

Конспект урока «Тепловые двигатели. Коэффициент полезного действия теплового двигателя (продолжение)»

В данной теме продолжаем решать задачи на тепловые двигатели и коэффициент полезного действия теплового двигателя. В частности подробно остановимся на решении задач, связанных с графиками тепловых процессов.

Задача 1. Одноатомный идеальный газ совершает цикл, состоящий из двух адиабат и двух изохор. В процессе адиабатного расширения 1—2 температура газа Т₂ = 0,75Т₁, а в процессе адиабатного сжатия 3—4 температура газа Т₃ = 0,75Т₄. Определите КПД цикла.

Коэффициент полезного действия цикла

Q₁ – количество теплоты, подведенное к газу;

Q₂ – количество теплоты, отведенное от газа.

Теплота к газу подводится в процессе 4–1 в количестве

Теплота отводится от газа в процессе 2–3 в количестве

Тогда КПД цикла

Ответ: КПД цикла составляет 25%.

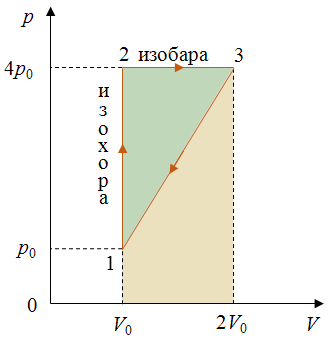
Задача 2. КПД теплового двигателя, рабочим телом которого является v моль одноатомного идеального газа, равен η. Газ совершает цикл, представленный на рисунке. Разность максимальной и минимальной температур газа в цикле равна ΔТ. Определите работу газа в изотермическом процессе.

Коэффициент полезного действия цикла равен

Процесс 1–2 является изотермическим и поэтому

Следовательно, из первого закона термодинамики

Процесс 2–3 является изохорным, следовательно работа расширения равна нулю

Тогда из первого закона термодинамики

Искомая работа газа равна

Задача 3. На рисунке изображен цикл, проводимый с одноатомным газом. Определите КПД этого цикла.

Запишем формулу для расчета коэффициента полезного действия цикла

Из графика видно, что при расширении работа, совершаемая газом, положительна и численно равна площади фигуры, ограниченной графиком 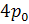, осью V и отрезками V–2 и 2V–3.

Работа, совершаемая при сжатии газа в ходе процесса 3–1, отрицательна и численно равна площади фигуры, ограниченной графиком процесса 3–1, осью V и отрезками V–1 и 2V–3.

Тогда, полезная работа газа за цикл, равна разности этих площадей

Из графика видим, что в процессе 1–2 происходит изохорное нагревание газа, а в процессе 2–3 — его изобарное расширение. Следовательно, в этих процессах газ получает теплоту

Из первого закона термодинамики следует

Так как работа газа зависит от вида процесса, то работа 1–2–3 равна сумме работ на участке 1–2 и участке 2–3

При изохорном процессе работа равна нулю

Изменение внутренней энергии

Тогда теплота, подведённая к газу

Ответ: КПД цикла равен 10,3%.

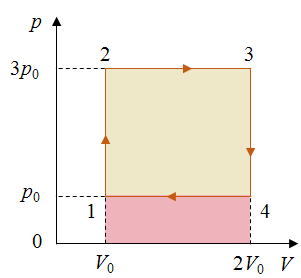
Задача 4. Тепловой двигатель, рабочим телом которого является идеальный газ, совершает цикл, изображенный на рисунке. Определите КПД двигателя.

Коэффициент полезного действия цикла

Полезная работа газа

Теплота подводится к газу в изохорном процессе 1–2 и в изобарном процессе 2–3. Согласно первому закону термодинамики эта теплота равна

Работа газа в процессе 1–2–3 равна сумме работ в процессах 1–2 и 2–3

Так как процесс 1–2 изохорный работа расширения газа равна нулю. Тогда работа в процессе 1–2–3

Внутренняя энергия является функцией состояния термодинамической системы и не зависит от того, каким образом система перешла в это состояние. Поэтому изменение внутренней энергии не зависит от вида процессов и равно разности ее значений в конечном и начальном состояниях

Т.к. из уравнения Менделеева-Клапейрона

Тогда количество теплоты, подведенное к газу

Ответ: КПД двигателя равен 19%.

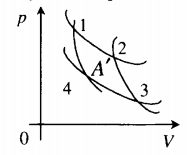
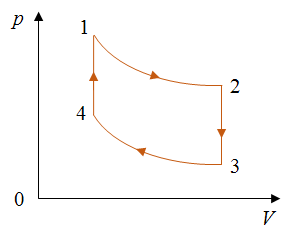
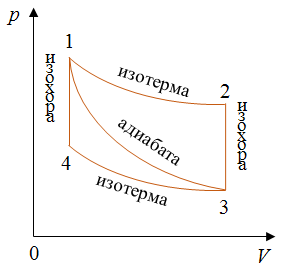
Задача 5. КПД тепловой машины в цикле 1—2—3—1 равен 50%, а в цикле 1—3—4—1 КПД равен 20%. Найдите КПД тепловой машины, работающей по циклу 1—2—3—4.

Из графика видно, что процессы 1–2 и 3–4 представляют собой изотермы.

График процесса 1–3 представляет собой адиабату, так как в этом случае давление газа уменьшается быстрее, чем при изотермическом процессе.

Процессы один-четыре и два-три происходят при неизменном объеме газа. Следовательно, это изохорные процессы.

Запишем формулу для определения коэффициента полезного действия для цикла 1–2–3–1

КПД для цикла 1–3–4–1

Т.к. процессы 2–3 и 4–1 изохорные, то подведенная теплота расходуется на изменение внутренней энергии. Температура газа в состояниях 1 и 2 одинакова, как и температура газа в состояниях 3 и 4. Следовательно, изменение внутренней энергии в процессах 2–3 и 4–1 одинаковое, а значит Q₄₁ = Q₂₃.

Тогда для цикла 1–2–3–4–1

Ответ: КПД тепловой машины, работающей по циклу 1—2—3—4 равен 40%.