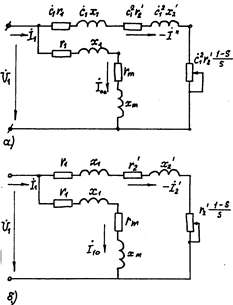
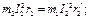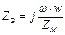Cхема замещения асинхронного электродвигателя

Трехфазные асинхронные электродвигатели, или как их еще называют индукционные электродвигатели, являются наиболее распространенными в промышленности. Данный тип электродвигателя, аналогично машинам постоянного тока тоже обладают свойствами обратимости, и может работать как в двигательном, генераторном, так и в тормозных режимах – противовключение, динамическое торможение. Режим работы асинхронного электродвигателя характеризуют знаком и величиной скольжения.

Пожалуй, основным методом анализа установившихся режимов индукционного электродвигателя является использование эквивалентных схем замещения. В таком случае обычно рассматривают явление, которое относится к одной фазе многофазного двигателя при соединении его обмоток звездой.

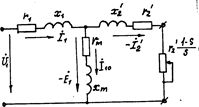
Упрощенная картина магнитных потоков работающего асинхронного электродвигателя позволяет представить его в виде эквивалентной схемы:

Электромагнитная связь первичной и вторичной цепи осуществляется потоком взаимоиндукции Ф, индуктирующим в роторной обмотке ЭДС Е₂S. Сопротивление индуктивное первичной цепи Х₁ обусловлено наличием потока рассеивания, связанного только с этой цепью. Аналогично сопротивления Х₂ обусловлено потоком рассеивания Ф₂₅.

Частота тока ротора будет определяться скоростью его вращения относительно скорости вращения магнитного поля статора, то есть зависеть от скольжения и будет равна f₂ = f₁S.

Ток вторичной цепи при вращающемся роторе:

Также выражения для I₂ может иметь:

Выше показанные выражения имеют не только различную форму записи, но и имеют совершенно разный физический смысл. А смысл его в том, что вместо вращающегося ротора можно рассматривать неподвижный, в котором будет индуцироваться ЭДС Е₂. При этом индуктивное сопротивление будет равно Х₂, а активное возрастет на величину так как . При этом I₁ останется прежним по фазе и величине, что не повлияет на потребляемую из сети мощность. Поскольку I₁ и I₂ не изменятся, то естественно и потери в первичных и вторичных цепях также не изменятся, соответственно мощность тоже не будет изменяться, а мощность развиваемая двигателем при вращении, будет равна мощности, потребляемой в добавочном сопротивлении . Таким образом, эквивалентная схема замещения асинхронной машины может быть заменена схемой замещения с добавочным сопротивлением r_д во вторичной цепи:

Т – образная схема замещения

После приведения первичной и вторичной ЭДС они будут равны Е₁ = Е₂ / и это дает возможность соединить эквивалентные точки и получить такую схему:

Недостатком Т – образной схемы замещения помимо сложностей расчета, является зависимость всех токов I₁, I₂ / , I_μ от скольжения s.

Из Т – образной схемы замещения видно, что в режиме холостого хода, при I₂ / = 0 и s = 0, ток в контуре будет обуславливаться сопротивлениями намагничивающего контура и первичной цепи и совсем не будет зависеть от скольжения. Данное обстоятельство позволит вынести на зажимы электродвигателя намагничивающий контур и перейти к Г – образной схеме замещения.

Г – образная схема замещения

Данная схема замещения позволяет изучать процессы в асинхронном электродвигателе, которые имеют место при изменении скольжения электрической машины.

Учет контура намагничивания необходим при определении I₁, который потребляется из сети. Но Г — образная схема замещения будет справедлива лишь при наличии определенных допущений:

• Все цепи имеют неизменные (постоянные) параметры. Это значит, что приведенное вторичное сопротивление r₂ / не будет зависеть от частоты цепи вторичной (ротора), а насыщение не будет влиять на реактивное сопротивление статорных и роторных обмоток Х₁ и Х₂ / ;
• Полная проводимость намагничивающего контура принимается неизменной, а ток намагничивания, независимо от нагрузки, будет всегда пропорционален напряжению, приложенному к обмоткам;
• Потери добавочные не учитываются;
• Паразитные моменты, создаваемые высшими гармониками МДС, также не учитывают.

Следует также помнить и то, что в Г – образной схеме замещения в величины сопротивлений необходимо внести соответствующие поправки:

В выше перечисленных уравнениях величины имеющие индекс «дейст» соответствуют реальным значениям параметров асинхронной машины, а без индексов – те, которые используют в эквивалентной схеме.

Поскольку отношение r₁/x_μ довольно таки мало, то практически довольно часто принимают:

Обычно δ лежит в пределах 1,05 – 1,1.

Первичный ток I₁ будет равен при любом скольжении:

Приведенный роторный ток:

Показанное выше выражение показывает, что ток ротора является функцией скольжения. При s = 0 I₂ / = 0. При увеличении скольжения I₂ / также будет расти, а при s = 1 достигнет своего максимума, или тока короткого замыкания, или пускового:

Если в роторной цепи отсутствует добавочное сопротивление (АД с КЗ ротором), пусковой ток может достигнуть довольно приличных значений, а именно 5 – 8 раз больше чем его номинальное значение.

Данная зависимость показана ниже:

Отношения пускового значения к номинальному является очень важным параметром для асинхронных машин с короткозамкнутым ротором, так как наличие пусковых токов приводит к просадкам напряжения, что особо ощутимо при использовании электродвигателей средней и большой мощности. Поэтому данная характеристика приводится в каталогах по выбору электрических машин.

Схемы замещения асинхронного двигателя переменного тока

Из принципа действия асинхронного двигателя известно, что для того чтобы ротор асинхронного двигателя пришел во вращение, обмотка ротора должна быть замкнута накоротко .

Как видно из схемы, асинхронный двигатель при разомкнутом роторе представляет собой трехфазный трансформатор в режиме холостого хода, следовательно, для расчета параметров асинхронного двигателя можно использовать схему замещения трансформатора.

Схема замещения трансформатора.

Как видно из формулы скольжения, оно будет изменяться в двигательном режиме от 1 до 0. Отсюда следует, что при работе асинхронного двигателя ток ротора будет изменяться в зависимости от режима работы, то есть в зависимости от скольжения. Двигатель будет работать только в том случае, когда обмотка ротора замкнута. Чтобы учесть в схеме замещения влияние нагрузки на ток I₂’, включаем в цепь ротора переменное сопротивление, равное по величине [(1-s)/s]·τ₂’.

Схема замещения асинхронного двигателя:

Схема замещения асинхронного двигателя.

Т-образная схема замещения двигателя:

Т-образная схема замещения асинхронного двигателя.

Т-образная схема замещения асинхронного двигателя не совсем точно отражает физические процессы, происходящие в асинхронном двигателе, и поэтому не может быть использована для расчета его параметров.

Чтобы учесть влияние тока нагрузки на напряжение между точками 1 и 2 выносим намагничивающий контур на зажимы статора двигателя. Получаем схему замещения, у которой намагничивающий контур не зависит от нагрузки.

Г-образная схема замещения:

Г-образная схема замещения асинхронного двигателя.

I₂’ – ток ротора, приведенный к статору.

Т-образная и Г-образная схемы замещения асинхронной машины

Как уже отмечалось, в неподвижном асинхронном двигателе электромагнитные процессы протекают, в основном так же, как в трансформаторе. В таком случае для анализа электромагнитных про­цессов в эквивалентной асинхронной машине с неподвижным ротором может быть использована Т-образная схема замещения трансформато­ра.

При составлении схемы замещения асинхронной машины рис.3 также, как в теории трансформаторов, обмотка ротора с числом фаз m₂ и числом витков в фазе w₂, заменяется приведенной об­моткой, имеющей число фаз m₁ и число витков фазы w₁, как у обмотки статора.

Рис.3. Т-образная схема замещения асинхронной машины.

Как и в трансформаторе при приведении параметров асинхрон­ной машины исходят из энергетического соответствия замещенной и реальной машин, но в асинхронной машине приведение параметров ро­тора к цепи статора несколько сложнее, чем в трансформаторе из-за пространственного распределения обмоток вдоль окружностей ротора и статора.

Так, из выражений (18) и (19) следует, что коэффициент при­ведения токов равен

Приведенная ЭДС Е / ₂ обмотки ротора должна быть равна ЭДС Е₁ об­мотки статора, тогда, используя выражения (11) и (12), получим

, (29)

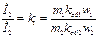
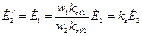
где 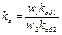— коэффициент приведения ЭДС. (30)

При приведении сопротивления r₂ исходят из того, что по­тери в активном сопротивлении ротора должны остаться без измене­ния. Тогда получим

, (31)

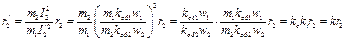
где k=k_e · k_i — коэффициент приведения сопротивлений.

При приведении индуктивного сопротивления рассеяния исходят из того, что угол ψ₂ между ЭДC E₂ и током I₂ остается неизменным

Для Т-образной схемы замещения асинхронной машины запишем уравнения напряжений и токов в виде

U₁= — Ė₁+Zİ₁ = — Ė₁ + r₁İ₁ + jx₁İ₁

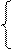
По своей структуре эта система уравнений аналогична системе ура­внений для трансформатора, к вторичной обмотке которого подклю­чено сопротивление нагрузки r_МЕХ=r₂’(1-S)/S. Количественное различие между схемами замещения асинхронной машины и трансформа­тора обусловлено значительно большим током холостого ходе асинхронной машины I₁₀=(0,25-0,5)I_1НОМ. Это объясняется наличием в магнитной цепи асинхронной машины воздушного зазора δ между статором и ротором, что приводит к увеличению магнитного сопроти­вления цепи и соответствующему уменьшению электрического сопротив­ления намагничивающей ветви схемы замещения. Это утверждение хо­рошо иллюстрируется формулой, выведенной Л.Р.Нейманом

где Z_Э — полное сопротивление контура намагничивания эквивалентной схемы замещения,

Z_М — полное магнитное сопротивление.

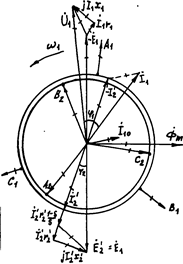
Системе уравнений (33) соответствует пространственно-времен­ная диаграмма асинхронной машины, приведенной к трансформатору. рис.4. По своему виду эта диаграмма похожа на диаграмму трансфор­матора. но имеет несколько более сложное физическое толкование. Диаграмма асинхронной машины изображается на комплексной плоскости, во-первых, для однопериодной модели, во-вторых, имеет две системы осей: одни оси связаны со статором, а вторые связаны с заторможенным в произвольном положении ротором (как правило, оси фаз статора не совпадают с осями фаз ротора).

При переходе от комплексных величин, изображенных векторами на комплексной плоскости, которые вращаются с угловой скоростью ω₁=2πf₁ / p, к мгновенным фазным величинам нужно спроектировать векторы статорных величин на оси фаз статора (A₁; B₁; C₁), а векторы роторных величин на неподвижные произвольно ориенти­рованные оси фаз ротора (A₂; B₂; C₂).

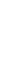
Рис.4. Пространственно-временная диаграмма асинхронной машины. P=1.

Итак, можно сделать вывод, что для исследования электромаг­нитных процессов в асинхронной машине может быть использована теория трансформаторов, что позволяет упростить задачу исследо­вания.

Т-образная схема замещения хорошо отражает реальные физиче­ские процессы, но при исследовании, например, механических характеристик асинхронной машины намного удобнее пользоваться вы­ражениями, которые содержат вместо ЭДС Е₁=E / ₂ напряжение сети U₁. В Т-образной

схеме замещения при изменения скольжения S изменяются не только токи I₁ и I / ₂, но и ток намагничивающего контура I₁₀, а следовательно, изменяется и ЭДC машины, в то время как напряжение сети остается постоянным независящим от нагрузки и режима работы.

В ряде случаев более удобной является другая, так называемая, Г-образная схема замещения асинхронной машины рис.5, в которой намагничивающая ветвь вынесена

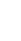
Рис.5. Г-образные схемы замещения асинхронной машины.

на зажимы с напряжением се­ти U₁. Для обоснования такой схемы замещения сделаем некоторые математические преобразования выражений, составленных по Т-образной схеме замещения асинхронной машины.

При синхронном вращении ротора и поля, т.е. в режиме идеального холостого хода асинхронной машины имеем: S=0; r / ₂(1-S)/S = ∞; İ / ₂=0; İ₁=İ₁₀. Для намагничивающей ветви Т-образной схемы замещения можно записать

Подставим значение ЭДС E₁ в уравнение напряжения (33), записанное для цепи статора в режиме идеального холостого хода,

Найдем отношение напряжения сети U₁ (35) к ЭДС E₁ (34) для идеального холостого хода асинхронной машины

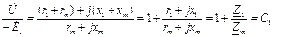
Комплексный коэффициент С₁ может быть представлен в алгебраической, показательной и

(37)

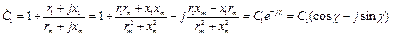
Мнимая часть комплексного числа С₁ обычно отрицательная, в свя­зи с чем аргумент χ имеет знак минус. Аргумент χ определя­ет угол поворота вектора ЭДC (-Е₁) относительно напряжения U₁. В связи с тем, что угол χ мал, например, в машинах, мощностью более 8 кВт угол χ // ₂ — преобразованный ток рабочей ветви Т-образной схемы замещения

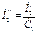Выразим ток İ // ₂ через напряжение сети U₁ и параметры асин­хронной машины. Для этого в системе уравнений (33) в уравнение напряжения, записанное для обмотки статора, подставим выражение ЭДС Е₁, составленное для обмотки ротора, получим уравнение для напряжения U₁ в виде

Преобразуем полученное уравнение с учетом выражений (40)-(42)

Из этого выражения найдем ток I // ₂

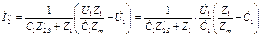или с учетом выражения (36)

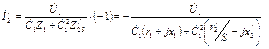Ток статора İ₁ найдем из уравнения (40) путем подстановки в это уравнение вместо токов İ₀₀ и İ // ₂ их выражений из (41) и (43)

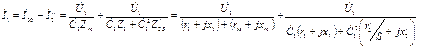В асинхронных машинах малой и средней мощности коэффициент С₁ близок к единице и равен С₁≈1,02-1,08.

Итак, уравнения (41), (43), (44), записанные для токов İ₀₀, İ // ₂, İ₁, соответствуют Г-образной схеме замещения рис.5а.

При анализе электромагнитных процессов в машинах общего применения часто по­лагают C₁≈1, что существенно облегчает расчеты и мало сказывается на точности конечных результатов расчета. Г-образную схему замещения при C₁=1 называют упрощенной схемой замещения с вынесенным намагничивающим контуром рис.5б. В этой схема без боль­шой погрешности можно принять, что в ветви намагничивания вместо тока İ₀₀ протекает ток İ₁₀, а в рабочей ветви вместо то­ка İ // ₂ — ток İ / ₂, как в Т-образной схеме замещения.