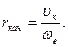РАДИУСЫ КАЧЕНИЯ КОЛЕСА



Автомобиль (трактор) движется в результате действия на него различных сил, которые делятся на движущие силы и силы сопротивления движению. Основной движущей силой является тяговая сила, приложенная к ведущим колесам. Тяговая сила возникает в результате работы двигателя и вызвана взаимодействием ведущих колес с дорогой. Тяговую силу Pк определяют как отношение момента на полуосях к радиусу ведущих колес при равномерном движении автомобиля. Следовательно, для определения тяговой силы необходимо знать величину радиуса ведущего колеса. Поскольку на колеса автомобиля устанавливаются эластичные пневматические шины, то величина радиуса колеса во время движения изменяется. В связи с этим различают следующие радиусы колес:
1.Номинальный – радиус колеса в свободном состоянии: rн=d/2+H, (6)
где d – диаметр обода, м;
H – полная высота профиля шины, м.
2.Статический rс – расстояние от поверхности дороги до оси нагруженного неподвижного колеса.
где λ–коэффициент радиальной деформации шины.
3.Динамический rд–расстояние от поверхности дороги до оси катящегося нагру женного колеса. Этот радиус увеличивается с уменьшением воспринимаемой нагрузки колесом Gк и увеличением внутреннего давления воздуха в шине pш.
При увеличении скорости автомобиля под действием центробежных сил шина растягивается в радиальном направлении, вследствие чего радиус rд увеличивается. При качении колеса изменяется и деформация поверхности качения в сравнении с неподвижным колесом. Поэтому плечо приложения равнодействующих касательных реакций дороги rд отличается от rс. Однако, как показали эксперименты, для практических тяговых расчетов можно принимать rс
4 Кинематический радиус (качения) колеса rк – радиус такого условного недеформирующегося кольца, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.
У колеса, катящегося под действием крутящего момента, элементы протектора, входящие в контакт с дорогой, сжаты, и колесо при равных частотах вращения проходит меньший путь, чем во время свободного качения; у колеса же, нагруженного тормозным моментом элементы протектора, входящие в контакт с дорогой, растянуты. Поэтому тормозное колесо проходит при равных числах оборотов несколько больший путь, чем свободно катящееся колесо. Таким образом, под действием крутящего момента радиус rк – уменьшается, а под действием тормозного момента – увеличивается. Для определения величины rк методом “меловых отпечатков” на дороге мелом или краской наносят поперечную линию, на которую накатывается колесо автомобиля, а затем оставляет на дороге отпечатки.
Замерив расстояние l между крайними отпечатками, определяют радиус качения по формуле: rк = l / 2π∙n , (8)
где n – частота вращения колеса, соответ ствующая расстоянию l .
В случае полного буксования колеса расстояние l = 0 и радиус rк = 0. Во время скольжения невращающихся колес (“ЮЗ”) частота вращения n=0 и rк 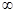
Радиусы качения колеса
Автомобиль (трактор) движется в результате действия на него различных сил, которые делятся на движущие силы и силы сопротивления движению. Основной движущей силой является тяговая сила, приложенная к ведущим колесам. Тяговая сила возникает в результате работы двигателя и вызвана взаимодействием ведущих колес с дорогой. Тяговую силу Pк определяют как отношение крутящего момента на полуосях к радиусу ведущих колес при равномерном движении автомобиля. Следовательно, для определения тяговой силы необходимо знать величину радиуса ведущего колеса. Поскольку на колеса автомобиля устанавливаются эластичные пневматические шины, то величина радиуса колеса во время движения изменяется. В связи с этим различают следующие радиусы колес:
1.Номинальный – радиус колеса в свободном состоянии: rн=d/2+H, (6)
где d – диаметр обода (посадочный диаметр шины), м;
H – полная высота профиля шины, м.
2.Статический rс – расстояние от поверхности дороги до оси нагруженного неподвижного колеса.
где λ–коэффициент радиальной деформации шины.
3.Динамический rд–расстояние от поверхности дороги до оси катящегося нагру женного колеса. Этот радиус увеличивается с уменьшением воспринимаемой нагрузки колесом Gк и увеличением внутреннего давления воздуха в шине pш.
При увеличении скорости автомобиля под действием центробежных сил шина растягивается в радиальном направлении, вследствие чего радиус rд увеличивается. При качении колеса изменяется и деформация поверхности качения в сравнении с неподвижным колесом. Поэтому плечо приложения равнодействующих касательных реакций дороги rд отличается от rс. Однако, как показали эксперименты, для практических тяговых расчетов можно принимать rс
Кинематический радиус (качения) колеса rк – радиус такого условного недеформирующегося кольца, которое имеет с данным эластичным колесом одинаковую угловую и линейную скорости.
У колеса, катящегося под действием крутящего момента, элементы протектора, входящие в контакт с дорогой, сжаты, и колесо при равных частотах вращения проходит меньший путь, чем во время свободного качения; у колеса же, нагруженного тормозным моментом элементы протектора, входящие в контакт с дорогой, растянуты. Поэтому тормозное колесо проходит при равных числах оборотов несколько больший путь, чем свободно катящееся колесо. Таким образом, под действием крутящего момента радиус rк – уменьшается, а под действием тормозного момента – увеличивается. Для определения величины rк методом “меловых отпечатков” на дороге мелом или краской наносят поперечную линию, на которую накатывается колесо автомобиля, а затем оставляет на дороге отпечатки.
Замерив расстояние l между крайними отпечатками, определяют радиус качения по формуле: rк = l / 2π∙n , (8)
где n – частота вращения колеса, соответствующая расстоянию l .
В случае полного буксования колеса расстояние l = 0 и радиус rк = 0. Во время скольжения не вращающихся колес (“ЮЗ”) частота вращения n=0 и rк 
Радиусы колес автомобиля
У колес автомобиля (рис. 3.4) различают следующие радиусы: статический rс, динамический rД и радиус качения rкач.
Статическим радиусом называется расстояние от оси неподвижного колеса до поверхности дороги. Он зависит от нагрузки, приходящейся на колесо, и давления воздуха в шине. Статический радиус уменьшается при возрастании нагрузки и снижении давления воздуха в шине, и наоборот.
Динамическим радиусом называется расстояние от оси катящегося колеса до поверхности дороги. Он зависит от нагрузки, давления воздуха в шине, скорости движения и момента, передаваемого через колесо. Динамический радиус возрастает при увеличении скорости движения и уменьшении передаваемого момента, и наоборот.
Радиусом качения называется отношение линейной скорости оси колеса к его угловой скорости:
Радиус качения, зависящий от нагрузки, давления воздуха в шине, передаваемого момента, пробуксовывания и проскальзывания колеса, определяется экспериментально или вычисляется по формуле
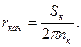
где nк — число полных оборотов колеса; SК — путь, пройденный колесом за полное число оборотов.
Из выражения (3.13) следует, что при полном буксовании колеса (Sk= 0) радиус качения rкач = 0, а при полном скольжении (nк = 0) гкач → оз.
Как показали исследования, на дорогах с твердым покрытием и хорошим сцеплением радиус качения, статический и динамический радиусы отличаются друг от друга незначительно. Поэтому можно
считать, что они практически равны, т. е. rс
При выполнении расчетов в дальнейшем будем использовать это приближенное значение. Соответствующую величину назовем радиусом колеса и обозначим rk.
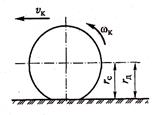
| Рис. 3.4. Радиусы колеса 31 |
ки и давления воздуха в шинах. Кроме того, радиус колеса, м, можно рассчитать по номинальным размерам шины, используя выражение
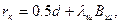
Рис. 3.4. Радиусы колеса
где d — диаметр обода колеса, м; Вш — ширина профиля шины, м; λш=0,8. 0,9 — коэффициент смятия шины.
Формула (3.14) обеспечивает наиболее точные результаты для самого распространенного типа шин — тороидальных.
Дата добавления: 2016-02-20 ; просмотров: 4332 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Радиусы эластичного колеса
В общем случае колесо автомобиля состоит из жесткого обода, эластичных боковин и контактного отпечатка. Контактный отпечаток шины представляет собой элементы шины, контактирующие с опорной поверхностью в рассматриваемый момент времени. Его форма и размеры зависят от типа шины, нагрузки на шину, давления воздуха, деформационных свойств опорной поверхности и ее профиля.
В зависимости от соотношения деформаций колеса и опорной поверхности возможны следующие виды движения:
— эластичного колеса по недеформируемой поверхности (движение колеса по дороге с твердым покрытием);
— жесткого колеса по деформируемой поверхности (движение колеса по рыхлому снегу);
— деформируемого колеса по деформируемой поверхности (движение колеса по деформируемому грунту, рыхлому снегу с пониженным давлением воздуха).
В зависимости от траектории возможны прямолинейное и криволинейное движения. Заметим, что сопротивление криволинейному движению превышает сопротивление прямолинейному. Это особенно касается трехосных автомобилей с балансирной задней тележкой. Так, при движении трехосного автомобиля по траектории с минимальным радиусом на дороге с высоким коэффициентом сцепления остаются следы от шин, с выхлопной трубы идет черный дым, резко увеличивается расход топлива. Все это является следствием возростания сопротивления криволинейному движению в несколько раз по сравнению с прямолинейным.
Ниже нами рассмотрены радиусы эластичного колеса для частного случая- при прямолинейном движении колеса на недеформируемой опорной поверхности.
Существуют четыре радиуса автомобильного колеса:
1) свободный; 2) статический; 3) динамический; 4) радиус качения колеса.
Свободный радиус колеса — характеризует размер колеса в ненагруженном состоянии при номинальном давлении воздуха в шине. Этот радиус равен половине наружного диаметра колеса
где rc – свободный радиус колеса в м;
Дн – наружный диаметр колеса в м, который определяется экспериментально при отсутствии контакта колеса с дорогой и номинальном давлении воздуха в шине.
В практике этот радиус используется конструктором для определения габаритных размеров автомобиля, зазоров между колесами и кузовом автомобилем при его кинематике.
Статический радиус колеса – расстояние от опорной поверхности до оси вращения колеса на месте. Определяется экспериментально или рассчитывается по формуле
где rcт – статический радиус колеса в м;
d – посадочный диаметр обода колеса в м;
lz— коэффициент вертикальной деформации шины. Принимается для тороидных шин lz=0,85…0,87; для шин регулируемого давления lz=0,8…0,85;
Н – высота профиля шины в м.
Динамический радиус колеса rd – расстояние от опорной поверхности до оси вращения колеса во время движения. При движении колеса по твердой опорной поверхности с малой скоростью в ведомом режиме принимается
Радиус качения колеса rк – путь, проходимый центром колеса, при его повороте на один радиан. Определяется по формуле
rк = 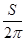
где S – путь, проходимый колесом за один оборот в м.;
2p — число радиан в одном обороте.
При качении колеса на него могут действовать крутящий Мкр и тормозной Мт моменты. При этом крутящий момент уменьшает радиус качения, а тормозной – увеличивает.
При движении колеса юзом, когда имеется путь и отсутствует вращение колеса, радиус качения стремится к бесконечности. Если происходит буксование на месте, тогда радиус качения равен нулю. Следовательно, радиус качения колеса изменяется от нуля до бесконечности.
Экспериментальная зависимость радиуса качения от приложенных моментов представлена на рис.3.1. На графике выделим пять характерных точек: 1,2,3,4,5.
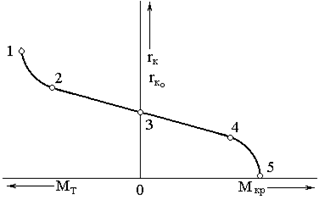
Участок 2-3-4 – условно ли-нейный, а точка 3 соответствует радиусу rко при качении колеса в ведомом режиме.
Радиус качения колеса на этом линейном участке определяется по формуле
где lт – коэффициент тангенциальной эластичности шины;
M — приложенный к колесу момент в Н.м.
Знак « + » брать, если к колесу приложен тормозной момент, а знак « — » — если крутящий.
На участках 1-2 и 4-5 не существует зависимостей для определения радиуса качения колеса.
Для удобства изложения материала в дальнейшем введем понятие «радиус колеса» rк,, имея ввиду следующее: если определяются параметры кинематики автомобиля (путь, скорость, ускорение), то под радиусом колеса понимается радиус качения колеса; если определяются параметры динамики (сила, момент), то под этим радиусом понимается динамический радиус колеса rd . С учетом принятого в дальнейшем динамический радиус и радиус качения будет обозначаться rк,
Дата добавления: 2016-05-11 ; просмотров: 4213 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ