Физика
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
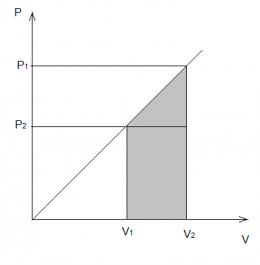
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p ( V ). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1 ; объем газа в конечном состоянии V 2 ). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
Если зависимость p ( V ) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе ( p = const) может быть вычислена по одной из формул:
A = p ∆ V , или A = ν R ∆ T ,
где p — давление газа; Δ V — изменение объема газа при переходе из начального в конечное состояние, Δ V = V 2 − V 1 ; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); Δ T — соответствующее изменение температуры газа, Δ T = T 2 − T 1 ; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе ( V = const) не совершается:
Работа газа при круговом ( циклическом ) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p ( V ). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2 , 3 — промежуточные состояния газа.
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
- положительной (прямой цикл);
- отрицательной (обратный цикл).
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p ( V ) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение . На рисунке изображен график циклического процесса в указанных термодинамических координатах p ( V ).
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A = 1 2 ( 125 − 75,0 ) ⋅ 10 3 ⋅ ( 0,0750 − 0,0250 ) = 1,25 ⋅ 10 3 Дж = 1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение . Запишем формулу для расчета работы смеси газов при изобарном процессе:
A = p ∆ V = p ( V 2 − V 1 ),
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
- парциальное давление водорода
p 1 = m 1 M 1 R T 1 V 1 ,
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
- парциальное давление гелия
p 2 = m 2 M 2 R T 1 V 1 ,
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
A = ( p 1 + p 2 ) ( V 2 − V 1 ) = ( m 1 M 1 R T 1 V 1 + m 2 M 2 R T 1 V 1 ) ( V 2 − V 1 ) .
Преобразование данного уравнения к виду
A = ( m 1 M 1 + m 2 M 2 ) R T 1 V 1 ( V 2 − V 1 ) = ( m 1 M 1 + m 2 M 2 ) R T 1 ( V 2 V 1 − 1 )
позволяет выразить искомое отношение объемов
V 2 V 1 = A ( m 1 M 1 + m 2 M 2 ) R T 1 + 1 .
V 2 V 1 = 46 ⋅ 10 3 ( 2,0 ⋅ 10 − 3 2,0 ⋅ 10 − 3 + 4,2 ⋅ 10 − 3 4,0 ⋅ 10 − 3 ) ⋅ 8,31 ⋅ 300 + 1 = 10 .
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
КПД теплового двигателя
В тепловых двигателях используется энергия сгорающего топлива. Однако, не вся энергия сгорающего топлива затрачивается на полезную работу, часть энергии безвозвратно рассеивается в окружающую среду.
Чем меньше эта утерянная часть теплоты, тем выше будет эффективность двигателя и его коэффициент полезного действия. Тем больше полезной работы сможет совершить газ при расширении, толкая поршень двигателя, или раскручивая диск газовой турбины.
Элементы тепловой машины
Конструкции тепловых машин отличаются разнообразием. Однако, из каких бы частей двигатель не состоял, он всегда содержит рабочее тело, холодильник и нагреватель (рис. 1).
Например, в двигателе внутреннего сгорания рабочим телом будут пары топлива и воздух.
В двигателе внутреннего сгорания роль нагревателя совместно выполняют свеча и поршень. Однако, поршень выполняет функции нагревателя только тогда, когда он сжимает газ. А свеча зажигает сжатый газ с помощью искры и вызывает горение топлива.
Чтобы передать остатки тепловой энергии атмосфере, двигатели с воздушным охлаждением имеют специальные ребристые поверхности на наружной части цилиндров.
А двигатели, в которых используется жидкостное (водяное) охлаждение, содержат насос, прокачивающий жидкость в специальных полостях двигателя и радиатор с вентилятором. Жидкость интенсивно охлаждается в радиаторе, а вентилятор обеспечивает обдув, чтобы ускорить охлаждение. Температура охлаждающей жидкости всегда выше температуры окружающего воздуха.
Какие функции выполняет каждый элемент
От нагревателя рабочее тело — газ, или пар, получает запас тепловой энергии (рис. 2). Затем, полученная энергия делится на две, как правило, неравные части. За счет одной части совершается работа.
А оставшаяся часть передается холодильнику (например, атмосфере) и рассеивается окружающей средой.
Роль холодильника в тепловом двигателе
Совершая работу, рабочее тело – расширяющийся газ, охлаждается. Температура \(T_
Так как газ, расширяясь, охлаждается, а при охлаждении энергию нужно куда-то девать, то никакая тепловая машина без холодильника работать не сможет. Чтобы функционировать, тепловая машина обязательно должна отдавать часть тепловой энергии холодильнику.
Обычно температура \(T_
Примечание: Паровой конденсатор применяется только в конструкциях паровых двигателей.
На какие части делится энергия нагревателя
Мы выяснили, что за счет одной части энергии газ совершает работу. Вторая часть полученной от нагревателя энергии передается холодильнику, который затем рассеивает ее в окружающее пространство (рис. 4).
Эта теплота выбрасывается в атмосферу вместе с отработанным паром, или сгоревшими выхлопными газами турбин и двигателей внутреннего сгорания – то есть, теряется безвозвратно. Главное то, что никакой газ не превращает свою внутреннюю энергию в работу полностью. Часть энергии неизбежно будет утеряна.
На полезную работу тратится только часть полученной энергии.
Посмотрев на рисунок 4, легко составить связь между энергией нагревателя, работой и энергией холодильника.
\(\large Q_
\(\large Q_
\(\large A \left(\text <Дж>\right) \) – работа, которую совершил расширяющийся газ (пар);
Так как часть энергии теряется, работа всегда будет меньше полученной энергии. Работу и энергию измеряют в джоулях. Работа – это затраченная энергия, то есть, разница между конечной и начальной энергией.
\[\large \boxed < Q_
Примечание: Полученная энергия берется со знаком «плюс», а утерянная – со знаком «минус». Нам уже известно, что энергия \(Q_
Формулы коэффициента полезного действия
Мы уже выяснили, что работа газа всегда меньше полученной теплоты. Чтобы ответить на вопрос, какую часть от полученной теплоты будет составлять работа, составим дробь:
\(\large A \left(\text <Дж>\right) \) – работа газа;
Эту дробь обозначают греческой буквой «эта» \(\eta\) и называют коэффициентом полезного действия (КПД). Так как этот коэффициент дает понятие о том, как соотносятся работа, совершенная газом и, полученная им тепловая энергия.
Числитель этой дроби всегда меньше знаменателя, математики такие дроби называют правильными. Если КПД теплового двигателя описывается правильной дробью, значит, он не может превышать единицу (рис. 5).
КПД теплового двигателя не превышает единицу, так как описывается правильной дробью.
Если подставить в числитель выражение для работы, получим развернутое выражение для вычисления КПД:
Правая часть уравнения – это две дроби, имеющие одинаковые знаменатели. Если записать правую часть в виде отдельных дробей, то можно получить такое соотношение:
Подставим его в выражение для КПД и получим еще одну формулу:
Какой максимальный КПД может иметь тепловой двигатель
Талантливый французский ученый и инженер Сади Карно в 1824 году придумал идеальную тепловую машину. В качестве рабочего тела в ней выступал идеальный газ. А сосуд, в который заключен газ, обернут теплоизоляцией, которую можно мысленно снять, когда возникнет такая необходимость.
Проведя мысленный эксперимент, Карно рассчитал, какую часть полученной энергии можно превратить в полезную работу при идеальных условиях. Другими словами, он рассчитал, какой максимально возможный КПД может иметь идеальный тепловой двигатель.
Для КПД идеального двигателя он получил такую формулу:
\(\large T_
\(\large T_
Из формулы следует:
Чем больше различаются температуры нагревателя и холодильника, тем выше будет КПД.
Если температура нагревателя сравняется с температурой холодильника, то полезной работы машина не совершит \(\large \eta = 0 \).
Максимальный КПД даже для идеального теплового двигателя всегда меньше единицы.
Температура холодильника не может равняться абсолютному нулю, так как достигнуть абсолютного нуля температуры не получается.
Примечание: В идеальном двигателе нет потерь энергии, так как полностью отсутствует трение между его движущимися частями. В реальных двигателях трение есть, поэтому КПД реальных двигателей всегда ниже, чем КПД идеального двигателя.
КПД реальных тепловых двигателей
КПД лучших образцов реальных двигателей, выпускаемых мировой промышленностью:
- паровых машин — менее 10 процентов.
- большинства двигателей внутреннего сгорания – до 30 процентов.
- газовых турбин — примерно 40 процентов.
- двигателя внутреннего сгорания Дизеля – около 44 процентов.
В настоящее время инженеры и ученые-физики работают над тем, чтобы в реальных двигателях уменьшить трение и потери тепловой энергии. Чтобы повысить давление в цилиндре, применяют дополнительные компрессоры и турбины. Это дает выигрыш еще в несколько процентов полезности, однако, сокращает срок службы таких двигателей.
Так называемые «атмосферники» — атмосферные двигатели внутреннего сгорания, в которых не применяются дополнительные турбины и компрессоры, повышающие рабочее давление в цилиндрах, могут без капитального ремонта прослужить на автомобилях весьма длительное время.
Некоторые автомобили, оснащенные особо удачными конструкциями двигателей, успевали без капитального ремонта двигателя проехать до 1 миллиона километров. Из-за этого, такие конструкции двигателей получили в народе название «миллионники». К сожалению, ныне выпуск подобных двигателей резко сокращен, из экономических соображений.
25. Молекулярная физика  Читать 0 мин.
Читать 0 мин.
25.225. Газовые циклы
При изменении объема газа, газ совершает работу.
При изобарическом процессе работа определяется как A = p∆V, где
Отсюда видно, что если объём газа не меняется, то есть ∆V = 0, то работа не совершается.
При расширении газа его работа положительна.
При сжатии газа работа отрицательна.
Работа, совершаемая газом, равна площади под графиком на PV диаграмме. На рисунке работа равна площади трапеции:
Внутренняя энергия идеального газа есть сумма кинетических энергий его частиц (энергией взаимодействия частиц пренебрегаем).
Внутренняя энергия идеального газа определяется формулой U = $\frac<3><2>\; kT$ , где:
T ― температура газа в Кельвинах [К],
k ― постоянная Больцмана, равная 1,38 10–23 [Дж/К].
Первое начало термодинамики представляет собой закон сохранения энергии, в применении к тепловым явлениям. Оно гласит, что тепло, полученное газом, идет на изменение внутренней энергии и совершение работы.
Q ― тепло, полученное газом [Дж],
∆U ― изменение внутренней энергии [Дж],
Адиабатический процесс — термодинамический процесс, при котором система не обменивается теплотой с окружающим пространством.
В первом начале термодинамики при адиабатическом процессе необходимо положить Q = 0.
Коэффициент полезного действия (КПД) — отношение полезно использованной энергии газа, ко всей полученной энергии:
η ― коэффициент полезного действия, КПД,
QH ― количество теплоты, полученное от нагревателя [Дж],
QX ― количество теплоты, отданное холодильнику [Дж].
Цикл Карно — максимально возможный КПД любой тепловой машины.
КПД цикла Карно определяется температурами нагревателя и холодильника.
η ― коэффициент полезного действия , КПД,
ТН ― температура нагревателя [К],
ТХ ― температура холодильника [К].








 Читать 0 мин.
Читать 0 мин.