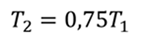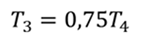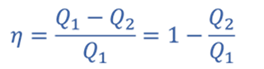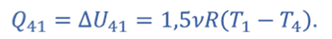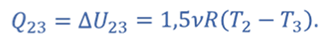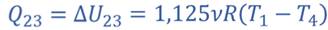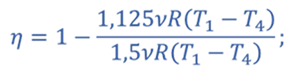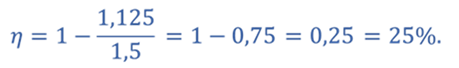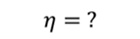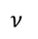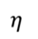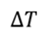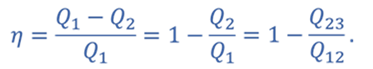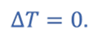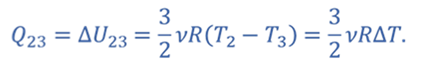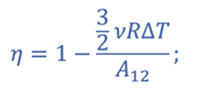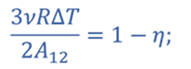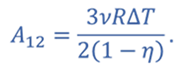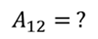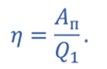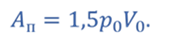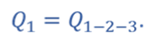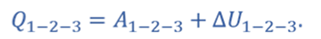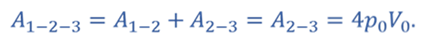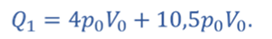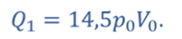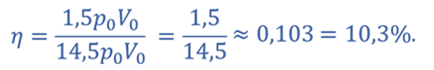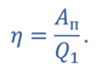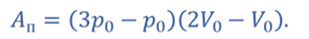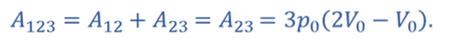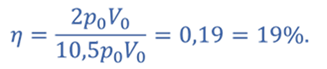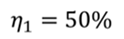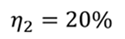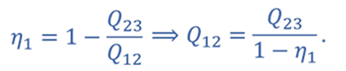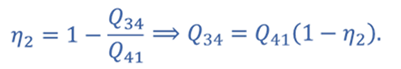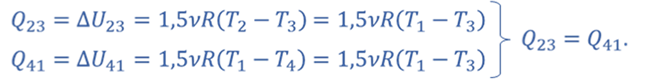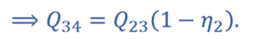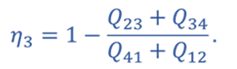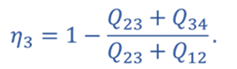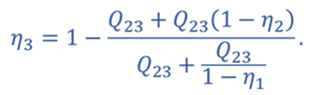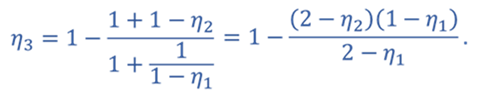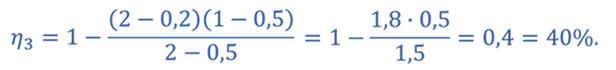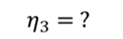Тепловые двигатели. Коэффициент полезного действия теплового двигателя (продолжение)

Урок 12. Решение задач по основам МКТ, оптике и квантовой физике

Конспект урока «Тепловые двигатели. Коэффициент полезного действия теплового двигателя (продолжение)»

В данной теме продолжаем решать задачи на тепловые двигатели и коэффициент полезного действия теплового двигателя. В частности подробно остановимся на решении задач, связанных с графиками тепловых процессов.

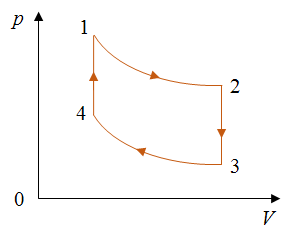
Задача 1. Одноатомный идеальный газ совершает цикл, состоящий из двух адиабат и двух изохор. В процессе адиабатного расширения 1—2 температура газа Т₂ = 0,75Т₁, а в процессе адиабатного сжатия 3—4 температура газа Т₃ = 0,75Т₄. Определите КПД цикла.

Коэффициент полезного действия цикла

Q₁ – количество теплоты, подведенное к газу;

Q₂ – количество теплоты, отведенное от газа.

Теплота к газу подводится в процессе 4–1 в количестве

Теплота отводится от газа в процессе 2–3 в количестве

Тогда КПД цикла

Ответ: КПД цикла составляет 25%.

Задача 2. КПД теплового двигателя, рабочим телом которого является v моль одноатомного идеального газа, равен η. Газ совершает цикл, представленный на рисунке. Разность максимальной и минимальной температур газа в цикле равна ΔТ. Определите работу газа в изотермическом процессе.

Коэффициент полезного действия цикла равен

Процесс 1–2 является изотермическим и поэтому

Следовательно, из первого закона термодинамики

Процесс 2–3 является изохорным, следовательно работа расширения равна нулю

Тогда из первого закона термодинамики

Искомая работа газа равна

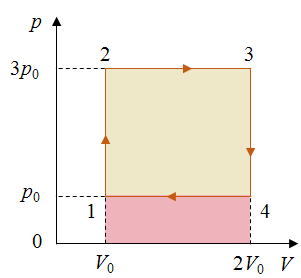
Задача 3. На рисунке изображен цикл, проводимый с одноатомным газом. Определите КПД этого цикла.

Запишем формулу для расчета коэффициента полезного действия цикла

Из графика видно, что при расширении работа, совершаемая газом, положительна и численно равна площади фигуры, ограниченной графиком 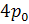, осью V и отрезками V–2 и 2V–3.

Работа, совершаемая при сжатии газа в ходе процесса 3–1, отрицательна и численно равна площади фигуры, ограниченной графиком процесса 3–1, осью V и отрезками V–1 и 2V–3.

Тогда, полезная работа газа за цикл, равна разности этих площадей

Из графика видим, что в процессе 1–2 происходит изохорное нагревание газа, а в процессе 2–3 — его изобарное расширение. Следовательно, в этих процессах газ получает теплоту

Из первого закона термодинамики следует

Так как работа газа зависит от вида процесса, то работа 1–2–3 равна сумме работ на участке 1–2 и участке 2–3

При изохорном процессе работа равна нулю

Изменение внутренней энергии

Тогда теплота, подведённая к газу

Ответ: КПД цикла равен 10,3%.

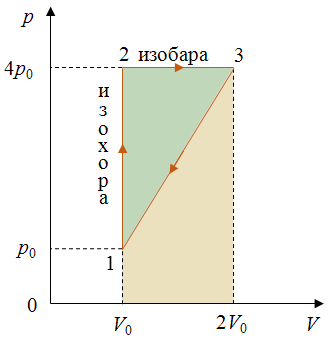
Задача 4. Тепловой двигатель, рабочим телом которого является идеальный газ, совершает цикл, изображенный на рисунке. Определите КПД двигателя.

Коэффициент полезного действия цикла

Полезная работа газа

Теплота подводится к газу в изохорном процессе 1–2 и в изобарном процессе 2–3. Согласно первому закону термодинамики эта теплота равна

Работа газа в процессе 1–2–3 равна сумме работ в процессах 1–2 и 2–3

Так как процесс 1–2 изохорный работа расширения газа равна нулю. Тогда работа в процессе 1–2–3

Внутренняя энергия является функцией состояния термодинамической системы и не зависит от того, каким образом система перешла в это состояние. Поэтому изменение внутренней энергии не зависит от вида процессов и равно разности ее значений в конечном и начальном состояниях

Т.к. из уравнения Менделеева-Клапейрона

Тогда количество теплоты, подведенное к газу

Ответ: КПД двигателя равен 19%.

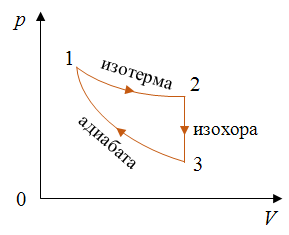
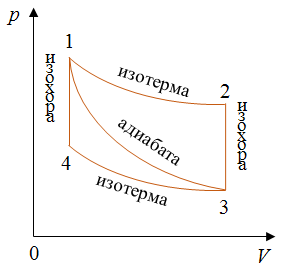
Задача 5. КПД тепловой машины в цикле 1—2—3—1 равен 50%, а в цикле 1—3—4—1 КПД равен 20%. Найдите КПД тепловой машины, работающей по циклу 1—2—3—4.

Из графика видно, что процессы 1–2 и 3–4 представляют собой изотермы.

График процесса 1–3 представляет собой адиабату, так как в этом случае давление газа уменьшается быстрее, чем при изотермическом процессе.

Процессы один-четыре и два-три происходят при неизменном объеме газа. Следовательно, это изохорные процессы.

Запишем формулу для определения коэффициента полезного действия для цикла 1–2–3–1

КПД для цикла 1–3–4–1

Т.к. процессы 2–3 и 4–1 изохорные, то подведенная теплота расходуется на изменение внутренней энергии. Температура газа в состояниях 1 и 2 одинакова, как и температура газа в состояниях 3 и 4. Следовательно, изменение внутренней энергии в процессах 2–3 и 4–1 одинаковое, а значит Q₄₁ = Q₂₃.

Тогда для цикла 1–2–3–4–1

Ответ: КПД тепловой машины, работающей по циклу 1—2—3—4 равен 40%.