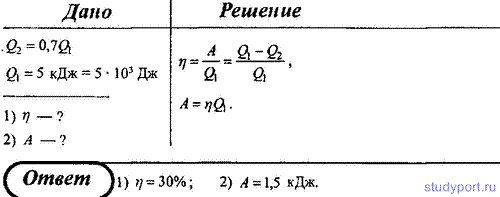Рабочее тело идеальный газ теплового двигателя совершает цикл состоящий

Чему равен КПД цикла, проводимого с идеальным одноатомным газом? Ответ приведите в процентах, округлить до целых.

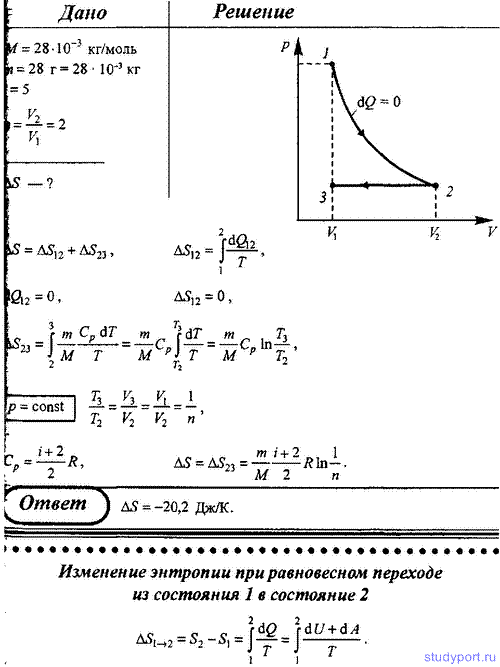
КПД тепловой машины определяется как отношение полезной работы и переданного рабочему телу тепла за цикл: Определим сперва полезную работу за цикл, на диаграмме этой величине соответствует площадь цикла: Передаваемое газу тепло рассчитаем при помощи первого начала термодинамики: Рассмотрим последовательно все участки цикла. На участке 1 — 2 газ не совершает работы, а изменение его внутренней энергии (с учетом уравнения Клапейрона-Менделеева) равно: Так как изменение внутренней энергии положительно, газ получает тепло на этом участке. На участке 2 — 3 газ совершает работу Изменение его внутренней энергии на этом участке: Следовательно, на этом участке газ получает тепло На участке 3 — 1 газ совершает отрицательную работу, он остывает, а значит, его внутренняя энергия уменьшается, следовательно, на этом участке он отдает тепло, а не получает. Окончательно, все полученное газом за цикл тепло равно Таким образом, КПД цикла равно

А разве здесь не нужно использовать формулу (дельта)U=Q+A, ведь над газом совершают работу, а не газ сам ее совершает. Или как вообще нужно определять в какой задаче какую формулу использовать, разве не нужно ориентироваться по дано задачи?

Формулу можно использовать любую, в зависимости от того, что Вам удобно в данной конкретной задаче. В данной задаче цикл идет по часовой стрелке, следовательно, газ совершает положительную работу, поэтому, возможно, удобнее использовать то, что использовано 🙂

Алексей! Поздравляю Вас. Вы очередной раз «изобрели» вечный двигатель второго рода. Обратите внимание на то, что в условии задачи указано, что газ одноатомный.

Если проделать те же вычисления с двухатомным газом, то значение КПД будет другим, что противоречит первой теореме Карно, которая гласит: «КПД обратимого цикла не зависит от рода вещества, из которого сделано рабочее тело».

Хотелось бы сделать одно замечание по поводу Ваших «тезисов». Один из них гласит: «Квазистатический (протекающий медленно) процесс обратим». Согласно ему, если дизельный двигатель медленно крутить в противоположном направлении, то в топливный бок потечет солярка, а из воздушного фильтра будет выходить очищенный воздух. Ведь, согласно Вашему тезису, все должно возвратиться в исходное положение Неужели Вы поверите этому бреду?!

Мне кажется, этот спор бесконечен. Мой тезис следующий, постараюсь его еще раз передать: «Если на некоторой диаграмме () задана точка, то состояние системы полностью задано и она находится в равновесном состоянии (мы считаем, что уравнение состояния нам известно). Если система не находится в равновесии, то точка на подобных диаграммах вообще не имеет смысла. Далее, когда на диаграмме нарисована линия, это последовательность равновесных состояний, через которые система проходит непрерывно, квазистатически. По линии можно перемещать систему в разных направлениях».

Что касается теоремы Карно, на которую Вы ссылаетесь, мне кажется, что Вы упускаете, существенный факт, что она формулируется для цикла Карно, когда есть нагреватель при одной температуре и холодильник при другой. Для цикла Крно получается все так, как Вы говорите. Но можно придумать огромную кучу оьратимых машин, отличных от машины Карно. Например, можно построить из адиабат и изотерм цикл с тремя температурами. Дальнейшее обобщение дает произвольную кривую. Я Вам уже рассказывал, что любую линию можно построить из адиабат и изотерм. Надеюсь в их обратимости Вы не сомневаетесь.

Ваш пример с двигателем, конечно, не вписывается в эту картину. Процесс превращения топлива в тепло с выбрасыванием продуктов горения нельзя обратить, как ни старайся.

Основы термодинамики

67. Азот, находившийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объем увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.

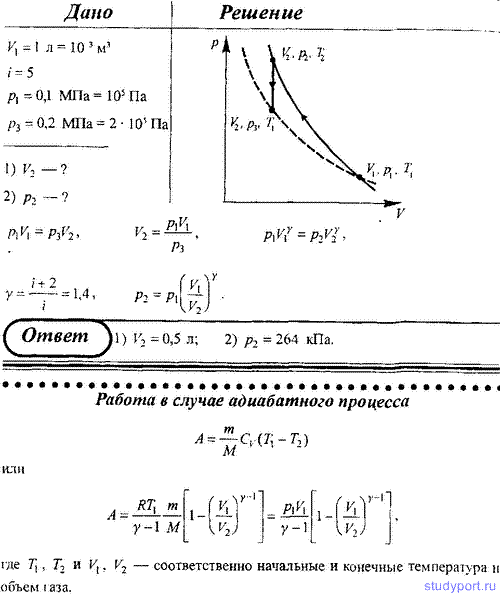
68. Двухатомный идеальный газ занимает объем V₁ = 1 л и находится под давлением p₁ = 0,1 МПа. После адиабатического сжатия газ занимает объем V₂ и создает давление p₂. В результате последующего изохорического процесса газ охлаждается до первоначальной температуры, а его давление p₃ = 0,2 МПа. Определите: 1) объем V₂ ; 2) давление p₂. Начертите график этих процессов.

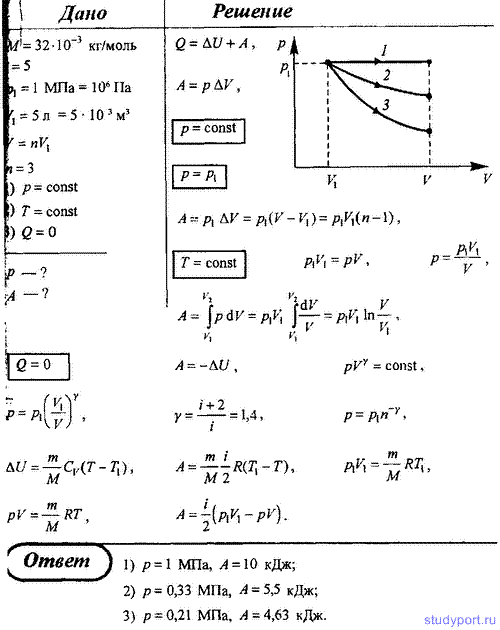
69. Кислород, занимающий при давлении p₁ = 1 МПа объем V₁ = 5 л, расширяется в n = 3 раза. Определите конечное давление и работу, совершенную газом в случае: 1) изобарного; 2) изотермического; 3) адиабатического процессов.

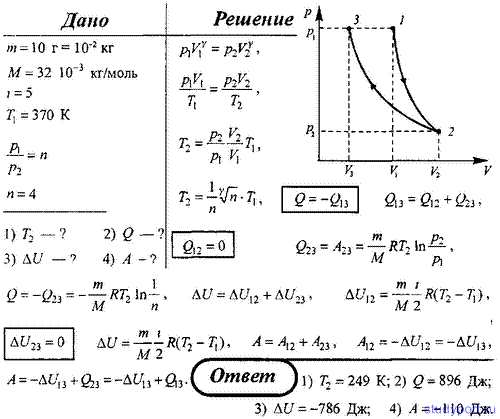
70. Кислород массой 10 г, находящийся при температуре 370 К, подвергли адиабатному расширению, в результате которого его давление уменьшилось в n= 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определите: 1) температуру газа в конце процесса; 2) количество теплоты, отданное газом; 3) приращение внутренней энергии газа; 4) работу, совершенную газом.

71. Идеальный двухатомный газ, занимающий объем V₁ = 2 л, подвергли адиабатному расширению. При этом его объем возрос в 5раз. Затем газ подвергли изобарному сжатию до начального объема В результате изохорного нагревания он был возвращен в первоначальное состояние. Постройте график цикла и определите термический КПД цикла.

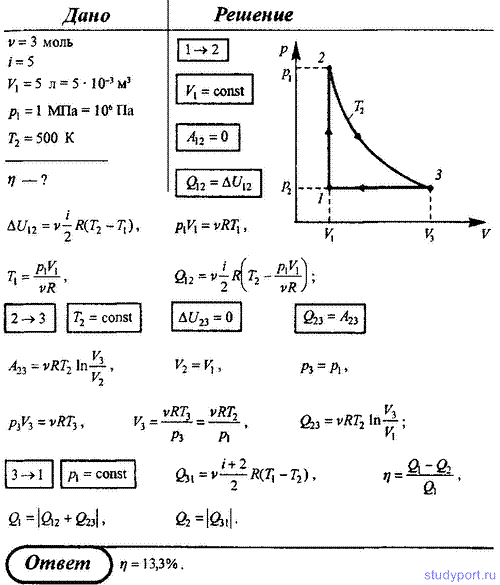
72. Идеальный двухатомный газ (ν=3 моль), занимающий объем V₁ = 5 л и находящийся под давлением p₁ = 1 МПа, подвергли изохорному нагреванию до Т₂ = 500 К. После этого газ подвергли изотермическому расширению до начального давления, а затем он в результате изобарического сжатия был возвращен в первоначальное состояние. Постройте график цикла и определите термический КПД цикла.

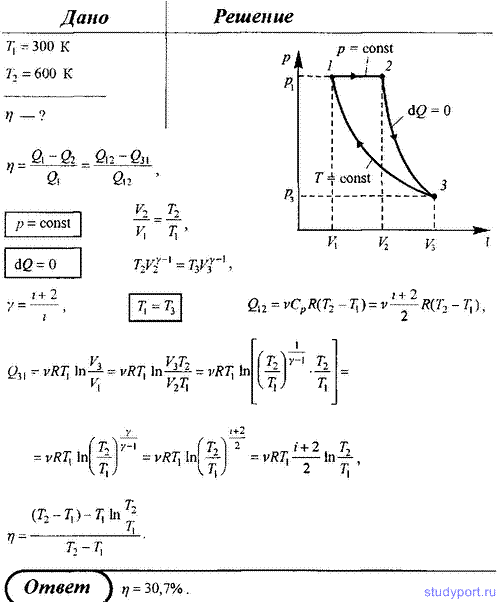
73. Рабочее тело – идеальный газ – совершает в тепловом двигателе цикл, состоящий из последовательных изобарического, адиабатического и изотермического процессов. В результате изобарного процесса газ нагревается от Т₁ = 300 К до Т₂ = 600 К. Определите термический КПД теплового двигателя.

74. Азот массой 500 г, находящийся под давлением p₁ = 1 МПа при температуре t₁ = 127 °С, подвергли изотермическому расширению, в результате которого давление газа уменьшилось в n = 3 раза. После этого газ подвергли адиабатному сжатию до начального давления, а затем он был изобарно сжат до начального объема. Постройте график цикла и определите работу, совершенную газом за цикл.

75. Идеальный газ, совершающий цикл Карно, 70% количества теплоты, полученного от нагревателя, отдает холодильнику. Количество теплоты, получаемое от нагревателя, равно 5 кДж. Определите: 1) термический КПД цикла; 2) работу, совершенную при полном цикле.

76. Идеальный газ совершает цикл Карно. Газ получил от нагревателя количество теплоты 5,5 кДж и совершил работу 1,1 кДж. Определите: 1) термический КПД цикла; 2) отношение температур нагревателя и холодильника.

77. Идеальный газ совершает цикл Карно, термический КПД которого равен 0,4. Определите работу изотермического сжатия газа, если работа изотермического расширения составляет 400 Дж.

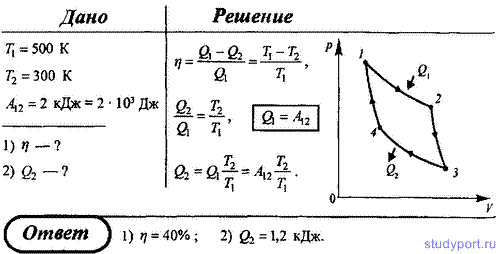
78. Идеальный газ совершает цикл Карно. Температура нагревателя Т₁ = 500 К, холодильника Т₂ = 300 К. Работа изотермического расширения газа составляет 2 кДж. Определите: 1) КПД цикла; 2) количество теплоты и отданное газом при изотермическом сжатии холодильнику.

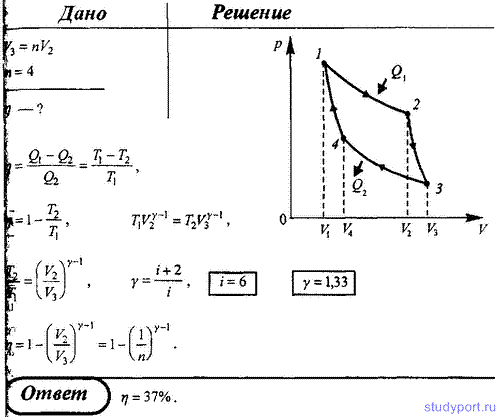
79. Многоатомный идеальный газ совершает цикл Карно, при этом в процессе адиабатного расширения объем газа увеличивается в n = 4 раза. Определите КПД цикла.

80. Во сколько раз необходимо увеличить объем (ν = 5 моль) идеального газа при изотермическом расширении, если его энтропия увеличилась на ΔS = 57,6 Дж/К?

81. При нагревании двухатомного идеального газа (ν = 2 моль) его термодинамическая температура увеличилась в n = 2 раза. Определите изменение энтропии, если нагревание происходит: 1) изохорно; 2) изобарно.

82. Идеальный газ (ν = 2 моль) сначала изобарно нагрели, так что объем газа увеличился в n = 2 раза, а затем изохорно охладили, так что давление его уменьшилось в n = 2 раза. Определите приращение энтропии в ходе указанных процессов.

83. Азот массой 28 г адиабатно расширили в n = 2 раза, а затем изобарно сжали до начального объема. Определите изменение энтропии газа в ходе указанных процессов.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

2.2 Основы термодинамики

UptoLike

Решебник Трофимова Т.И. (1999) — Задача 2. 73

Рабочее тело – идеальный газ – совершает в тепловом двигателе цикл, состоящий из последовательных изобарического, адиабатического и изотермического процессов. В результате изобарного процесса газ нагревается от Т1 = 300 К до Т2 = 600 К. Определите термический КПД теплового двигателя.

Решебник Трофимова Т.И. (1999) — Задача 2. 72

Идеальный двухатомный газ (ν = 3 моль), занимающий объем V1 = 5 л и находящийся под давлением p1 = 1 МПа, подвергли изохорному нагреванию до Т2 = 500 К.

Решебник Трофимова Т.И. (1999) — Задача 2. 71

Идеальный двухатомный газ, занимающий объем V1 = 2 л, подвергли адиабатному расширению. При этом его объем возрос в 5 раз. Затем газ подвергли изобарному сжатию до начального объема В результате изохорного нагревания он был возвращен в первоначальное состояние.

Решебник Трофимова Т.И. (1999) — Задача 2. 70

Кислород массой 10 г, находящийся при температуре 370 К, подвергли адиабатному расширению, в результате которого его давление уменьшилось в n = 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления.

Решебник Трофимова Т.И. (1999) — Задача 2. 69

Кислород, занимающий при давлении p1 = 1 МПа объем V1 = 5 л, расширяется в n = 3 раза. Определите конечное давление и работу, совершенную газом в случае: 1) изобарного; 2) изотермического; 3) адиабатического процессов.

Решебник Трофимова Т.И. (1999) — Задача 2. 68

Двухатомный идеальный газ занимает объем V1 = 1 л и находится под давлением p1 = 0,1 МПа. После адиабатического сжатия газ занимает объем V2 и создает давление p2. В результате последующего изохорического процесса газ охлаждается до первоначальной температуры, а его давление p3 = 0,2 МПа.

Решебник Трофимова Т.И. (1999) — Задача 2. 67

Азот, находившийся при температуре 400 К, подвергли адиабатическому расширению, в результате которого его объем увеличился в n = 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определите массу азота.

Решебник Трофимова Т.И. (1999) — Задача 2. 66

Азот массой m = 1 кг занимает при температуре T1 = 300 К объем V1 = 0,5 м3. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определите: 1) конечный объем газа; 2) его конечную температуру; 3) изменение внутренней энергии газа.

Решебник Трофимова Т.И. (1999) — Задача 2. 65

При адиабатном расширении кислорода (ν = 2 моль), находящегося при нормальных условиях, его объем увеличился в n = 3 раза. Определите: 1) изменение внутренней энергии газа; 2) работу расширения газа.

Рабочее тело идеальный газ теплового двигателя совершает цикл состоящий

На pV-диаграмме показан циклический процесс, состоящий из двух изохор и двух адиабат. В качестве рабочего вещества используется одноатомный идеальный газ.

Из приведённого ниже списка выберите два правильных утверждения.

1) Данный цикл соответствует циклу идеальной тепловой машины (циклу Карно).

2) В процессе 4–1 газ получил количество теплоты 450 Дж.

3) В процессе 2–3 газ отдал в 4 раза большее количество теплоты, чем получил в процессе 4–1.

4) Внутренняя энергия газа в процессе 1–2 уменьшается.

5) В процессах 1–2 и 3–4 газ не совершает работы.

Проверим правильность утверждений.

1) Цикл Карно состоит из двух изотерм и двух адиабат. Утверждение 1 — неверно.

2) Согласно первому началу термодинамики, переданное газу тепло идёт на изменение его внутренней энергии и на совершение работы против внешних сил: Процесс 4–1 является изохорный, а значит, работа газа в нём равна нулю. Газ получил

Утверждение 2 — верно.

3) В процессе 2–3 объём газа в 4 раза больше, а вот давление изменяется меньше, чем в процессе 4–1. Утверждение 3 — неверно.

4) Адиабата всегда идёт круче чем изотерма. При этом, чем выше находится изотерма на pV-диаграмме, тем выше температура газа. Отсюда делаем вывод, что температура газа в состоянии 1 выше чем в состоянии 2, следовательно, в процессе 1–2 внутренняя энергия уменьшилась. Утверждение 4 — верно.

5) Объём газа в процессах 1–2 и 3–4 изменяется, а значит, газом или над газом совершается работа. Утверждение 5 — неверно.

На рисунке показаны pT-диаграммы двух циклических процессов, совершаемых с одним и тем же постоянным количеством идеального газа. Некоторая тепловая машина сначала осуществляет цикл 1−2−3−4−1, а затем — цикл 5−6−7−8−5.

Используя рисунок, определите, как изменятся указанные в таблице физические величины при переходе тепловой машины от функционирования по циклу 1−2−3−4−1 к функционированию по циклу 5−6−7−8−5.

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Как видно из графика, оба цикла состоят из двух изобар и двух изохор. Используя уравнение Менделеева-Клапейрона, изобразим эти процессы на pV-диаграмме:

Работа газа за цикл численно равна площади фигуры, ограниченной графиком цикла. Как видно из графика, площади фигур равны в обоих циклах, а значит и совершаемая газом работа не изменилась.

Изобарное сжатие происходит в процессах 4−1 и 8−5. Таким образом, модуль работы в процессе изобарного сжатия уменьшается.

Многие сельские дома отапливаются в настоящее время при помощи электрообогревателей, что обходится достаточно дорого. При этом совершаемая электрическим током работа А превращается в равное ей количество теплоты Q, и батареи отопления нагреваются до температуры Т₁ = 60 °С. Однако расходы можно значительно снизить, если использовать эту работу A для перекачки теплоты Q_хол от внешнего теплового резервуара, имеющего температуру Т₂ = 0 °С (например, от незамерзающего зимой пруда), к батареям, выделяя в них количество теплоты Q_нагр. Во сколько раз n при этом количество теплоты Q_нагр превышает Q = А, если перекачивающее теплоту устройство работает по идеальному циклу Карно, запущенному в обратном направлении, а температура батарей остаётся равной Т₁? Считайте, что в идеальной тепловой машине все процессы обратимые, так что при запуске её в обратном направлении знаки всех энергетических вкладов (работы и количеств теплоты) просто поменяются, а соотношения между ними останутся прежними.

1. Согласно первому закону термодинамики, Здесь мы считаем все величины положительными, а знаки разных вкладов учитываем при написании уравнений.

2. Согласно второму закону термодинамики, КПД идеальной тепловой машины, работающей по циклу Карно, откуда где

3. В идеальной тепловой машине все процессы обратимые. Как указано в условии задачи, при запуске её в обратном направлении знаки всех энергетических вкладов просто поменяются, а соотношения между ними останутся прежними. В частности, из написанных уравнений следует, что

4. Окончательно получаем: Это очень выгодно по сравнению с простыми электрообогревателями, КПД которых равен единице!

Ответ:

Многие дачные дома отапливаются в настоящее время при помощи электрообогревателей, что обходится достаточно дорого. При этом совершаемая электрическим током работа А превращается в равное ей количество теплоты Q, и батареи отопления нагреваются до температуры Т₁ = 50 °С. Однако расходы можно значительно снизить, если использовать эту работу A для перекачки теплоты Q_хол от внешнего теплового резервуара, имеющего температуру Т₂ = 4 °С (например, от дна незамерзающего зимой пруда), к батареям, выделяя в них количество теплоты Q_нагр. Во сколько раз n при этом количество теплоты Q_нагр превышает Q = А, если перекачивающее теплоту устройство работает по идеальному циклу Карно, запущенному в обратном направлении, а температура батарей остаётся равной Т₁? Считайте, что в идеальной тепловой машине все процессы обратимые, так что при запуске её в обратном направлении знаки всех энергетических вкладов (работы и количеств теплоты) просто поменяются, а соотношения между ними останутся прежними.

1. Согласно первому закону термодинамики, Здесь мы считаем все величины положительными, а знаки разных вкладов учитываем при написании уравнений.

2. Согласно второму закону термодинамики, КПД идеальной тепловой машины, работающей по циклу Карно, откуда где

3. В идеальной тепловой машине все процессы обратимые. Как указано в условии задачи, при запуске её в обратном направлении знаки всех энергетических вкладов просто поменяются, а соотношения между ними останутся прежними. В частности, из написанных уравнений следует, что

4. Окончательно получаем: Это очень выгодно по сравнению с простыми электрообогревателями, КПД которых равен единице!

Ответ: