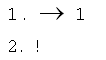Основные составные части машины поста

Теоретическая часть. Состав машины Поста

Машина Поста состоит из ленты и каретки (называемой также считывающей изаписывающей головкой). Лента бесконечна и разделена на секции одинакового размера — ячейки.

Рис. 1. В каждый момент времени каретка указывает на одну из ячеек

В каждой ячейке ленты может быть либо ничего не записано, либо стоять меткаV. Информация о том, какие ячейки пусты, а какие содержат метки, образуетсостояние ленты. Иными словами, состояние ленты — это распределение меток по ячейкам. Состояние ленты меняется в процессе работы машины. Заметим, что наличие метки в ячейке можно интерпретировать как “1”, а отсутствие — “0”. Такое двоичное представление информации подобно представлению, используемому практически во всех современных ЭВМ.

Каретка может передвигаться вдоль ленты влево и вправо. Когда она неподвижна, она стоит против ровно одной ячейки ленты; говорят, что каретка обозревает одну ячейку. За единицу времени каретка может совершить одно из трех действий: стереть метку, поставить метку, совершить движение на соседнюю ячейку.Состояние машины Поста складывается из состояния ленты и положения каретки.

Действия каретки подчинены программе, состоящей из перенумерованного набора команд (команды можно представлять как строки программы). Команды бывают шести типов:

1. записать 1 (метку), перейти к i-й строке программы;

2. записать 0 (стереть метку), перейти к i-й строке программы;

3. сдвиг влево, перейти к i-й строке программы;

4. сдвиг вправо, перейти к i-й строке программы;

6. если 0, то перейти к i, иначе перейти к j.

Приведем список недопустимых действий, ведущих к аварийной остановке машины:

попытка записать 1 (метку) в заполненную ячейку;
попытка стереть метку в пустой ячейке;
бесконечное выполнение (вообще говоря, это трудно назвать аварийным остановом, но бессмысленное повторение одних и тех же действий — зацикливание — ничуть не лучше вышеперечисленного).

Машина Поста, несмотря на внешнюю простоту, может производить различные вычисления, для чего надо задать начальное состояние каретки и программу, которая эти вычисления сделает. Машиной эта математическая конструкция названа потому, что при ее построении используются некоторые понятия реальных машин (ячейка памяти, команда и др.). Условимся каждый шаг программы обозначать номером. Команды машины будем обозначать следующим образом:

Будем говорить, что мы можем применить программу к текущему состоянию машины Поста, если выполнение программы не приведет к зацикливанию, т.е. рано или поздно мы выполним команду останов.

Пример программы, которая не применима ни к одному состоянию машины Поста:

Рассмотрим задачу для машины Поста и ее решение.

Задача.На ленте проставлена метка в одной-единственной ячейке. Каретка стоит на некотором расстоянии левее этой ячейки. Необходимо подвести каретку к ячейке, стереть метку и остановить каретку слева от этой ячейки.

Решение. Сначала попробуем описать алгоритм обычным языком. Поскольку нам известно, что каретка стоит напротив пустой ячейки, но неизвестно, сколько шагов нужно совершить до пустой ячейки, мы можем сразу сделать шаг вправо; проверить, заполнена ли ячейка; если она пустая, то повторять эти действия до тех пор, пока не наткнемся на заполненную ячейку. Как только мы ее найдем, мы выполним операцию стирания, после чего нужно будет лишь сместить каретку влево и остановить выполнение программы.

Программа для машины Поста:

Практическая часть практикума “Машина Поста”

Все задачи практикума сгруппированы по темам. Начинать знакомство с машиной Поста рекомендуется с первой темы “Применимость программ. Определение результата выполнения программ”.

Пояснения к условиям задач

1) В задачах под массивом понимается последовательность подряд идущих меток, ограниченная пустыми ячейками.

2) Если в задаче говорится, что на ленте задано число в унарной системе, то имеется в виду, что натуральное число n закодировано с помощью массива длиныn.

3) В задачах при описании начального состояния ленты будем указывать то, что записано начиная с самой левой непустой ячейки и заканчивая самой правой непустой ячейкой. При этом будем использовать следующие обозначения: nподряд идущих меток будем обозначать 1n, а m пустых ячеек — 0m. При обозначении одной заполненной или пустой ячейки будем писать просто 1 или 0, соответственно.

К примеру, запись “12012” будет соответствовать записи “11011” на ленте.

4) Если не сказано ничего о местонахождении каретки в начальный момент времени, то будем считать, что каретка обозревает ячейку с самой левой меткой.

Дата добавления: 2015-01-05 ; просмотров: 24 ; Нарушение авторских прав

Теория алгоритмов. Машина Поста
статья по информатике и икт (10 класс)

В статье анализируется возможность преобразования классической машины Поста в её многомерную вариацию.

Ключевые слова: машина Поста, алгоритмизация, конечные автоматы, клеточные автоматы, машина Тьюринга.

Скачать:

Читайте также:

I. СОСТАВ И ОБЪЕМ ПРОЕКТА.
I.5.3) Составные части Свода Юстиниана (общая характеристика).
III.11. ТЕОРЕТИЧЕСКАЯ ПЛОТНОСТЬ
IV. Магическая сила правильной постановки вопросов
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 1 страница
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 10 страница
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 11 страница
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 12 страница
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 13 страница
NB! НачинайтеРАЗБОР ПО СОСТАВУ глагольной формы не с окончания, а С ОСНОВЫ (т.е. одной из словарных основ). Вспомните известную фразу: ЗРИ В КОРЕНЬ! 14 страница

Вложение	Размер
teoriya_algoritmov._mashina_posta.docx	89.89 КБ

Предварительный просмотр:

Теория алгоритмов. Машина Поста.

Машина Поста — абстрактная вычислительная машина, предложенная Эмилем Леоном Постом, которая отличается от машины Тьюринга большей простотой. Обе машины алгоритмически «эквивалентны» и были придуманы для уточнения понятия

Машина Поста состоит из каретки (или считывающей и записывающей головки) и разбитой на ячейки бесконечной в обе стороны ленты (см. пример ниже). Каждая ячейка ленты может находиться в 2 состояниях — быть либо пустой — 0 , либо помеченной меткой 1 . За такт работы машины каретка может сдвинуться на одну позицию влево или вправо, считать, изменить символ в своей текущей позиции.

Работа машины Поста определяется программой, состоящей из конечного числа строк. Для работы машины нужно задать программу и её начальное состояние (то есть состояние ленты и позицию каретки). Кареткой управляет программа, состоящая из пронумерованных не обязательно упорядоченных строк команд, если в каждой команде указана строка, на которую нужно перейти. Обычно принимается, что если в команде переход не указан, то переход происходит на следующую строку [1].

Машины Тьюринга и Поста классифицируются следующим образом. По отношению к случайности: детерминированные, недетерминированные, стохастические. По количеству лент: одноленточные, многоленточные. По свойствам ленты: ленты, бесконечные в оба направления, ленты, бесконечные в одном направлении. Также, я предлагаю классифицировать по двум другим признакам. Так как при переходе с ленты на некое n-мерное поле, наблюдаются изменения в способах программирования. Таким образом, предлагается добавить классификацию по свойствам поля (одномерное, многомерное) и по количеству кареток (однокареточная, многокареточная), так как это также сильно влияет на работу с машиной.

Целью представляемой работы было показать сводимость (или же принципиальную несводимость) многомерной (многокареточной) машины Поста к одноленточной (однокареточной). Что значит показать полноту многомерной (многокареточной) машины Поста по Тьюринга [2]. Поскольку, в случае неполноты по Тьюрингу, мы получаем новую машину с новыми свойствами, которая в состоянии, вероятно, сильно упрощать алгоритмы. Классическая машина Поста является полной по Тьюрингу [3]. Таким образом, следует показать лишь сводимость к ней многомерной машины Поста.

Кроме того, интерес заключается в том, что многомерная машина Поста и клеточные автоматы по многим признакам похожи.

Клеточный автомат может мыслиться как стилизованный мир. Пространство представлено равномерной сеткой, каждая ячейка которой, или клетка, содержит

несколько битов данных; время идет вперед дискретными шагами, а законы мира выражаются единственным набором правил [4].

Такое исследование представилось интересным также благодаря следующим причинам: схожесть систем (обе имеют бесконечное поле, возможный алфавит из 0 и 1, возможность описания правил) [5]; машина Поста с двухмерным полем и двумя каретками имеет хороший потенциал к сжатию данных; не было обнаружено исследований такого рода, проведённых кем-либо ранее.

А клеточные автоматы, в свою очередь, представляют интерес для криптографии.

Ведь сейчас появляется всё больше блочных алгоритмов шифрования на их основе.

Итак, первое, что нам придётся использовать это теорема: для любой машины Тьюринга существует машина Тьюринга, работающая на полубесконечной ленте [6]. Поскольку машина Тьюринга и Поста эквивалентны, то применим данную теорему к машине Поста.

Рис. 1. Эквивалентность двухленточной и одноленточной машины Поста

Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Поста может быть построена эквивалентная машина Поста с объявленным свойством. Во-первых, произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте. Затем перенумеруем ячейки, причём будем считать, что символ «*» не содержится в словаре. Наконец, изменим машину Поста, удвоив число её состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна её работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МП встретится символ ‘*’, значит головка считывания-записи достигла границы зоны. Получим следующую карту состояний.

Рис. 2. Состояния МП при переходе к полубесконечному виду

Далее требуется перейти к многомерному полю. Для простоты рассмотрим на ограниченном отрезке.

Рис. 3. Соответствие полубесконечной МП и МП с двухмерным полем

Отметим отдельно, что асимметричная нумерация верхней и нижней частей полубесконечной (многоленточной машины) необходима, так как иначе невозможно будет полностью отразить расположение и состояние всех «зажженных» клеток многомерной машины Поста. Однако, несмотря на такое преобразование, это не влияет на предполагаемую эквивалентность полубесконечной машины Поста и машины Поста с многомерным полем. Для простоты восприятия ленты на рис. 3 выделены белым и серым цветами.

Для использования в МП многомерного поля требуется задать новые опции движения кареток. Таким образом, при двухмерному поле, добавим варианты движения вверх и вниз. Пронумеровав ленту и поле таким образом, как видно на рис. 3, мы сможем задать правила перехода. Движение по верхней (серой) ленте полубесконечной МП будет соответствовать движению каретки на поле вправо и влево (счёт столбцов). Движение по нижней (белой) ленте будет соответствовать движению каретки вверх и вниз по полю (счёт строк).

На рис. 3 видно, что правило для соответствия предполагает использование двух меток вместо одной. Таким образом, учитывая предыдущее, для перобразования в одноленточную МП многомерной, потребуется уменьшение сложности программы в 4 раза. Так как мы удвоили количество состояний при переходе от одноленточной МП к полубесконечной. Затем усложнили правила (введение новых свободностей движения) для перехода к многомерной. Также, при добавлении кареток, исходная МП усложняется в два раза за каждую новую каретку (соответственно программа на многомерной многокареточной машине упрощается).

Из вышестоящего получается, что использование многомерной многокареточной машины Поста возможно лишь для упрощения программирования и дальнейшего сопоставления с классической, так как принципиально новых эффектов при использовании такой конфигурации не обнаружено. Выявлено лишь упрощение программы благодаря внесённым при конфигурировании новым правилам.

Успенский В.А. Машина Поста / Гл. ред. физ.-мат. лит. 2-е изд., испр. М.: Наука, 1988. 96 с.
Brainerd W.S., Landweber L.H. Theory of Computation. Wiley, 1974. 278 p.
Neary T. , Woods D. Four small universal / Turing machines. / Fundamenta Informaticae,