Что такое момент инерции: формулы для стержня и колеса
Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения. Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.
Вращение и момент инерции
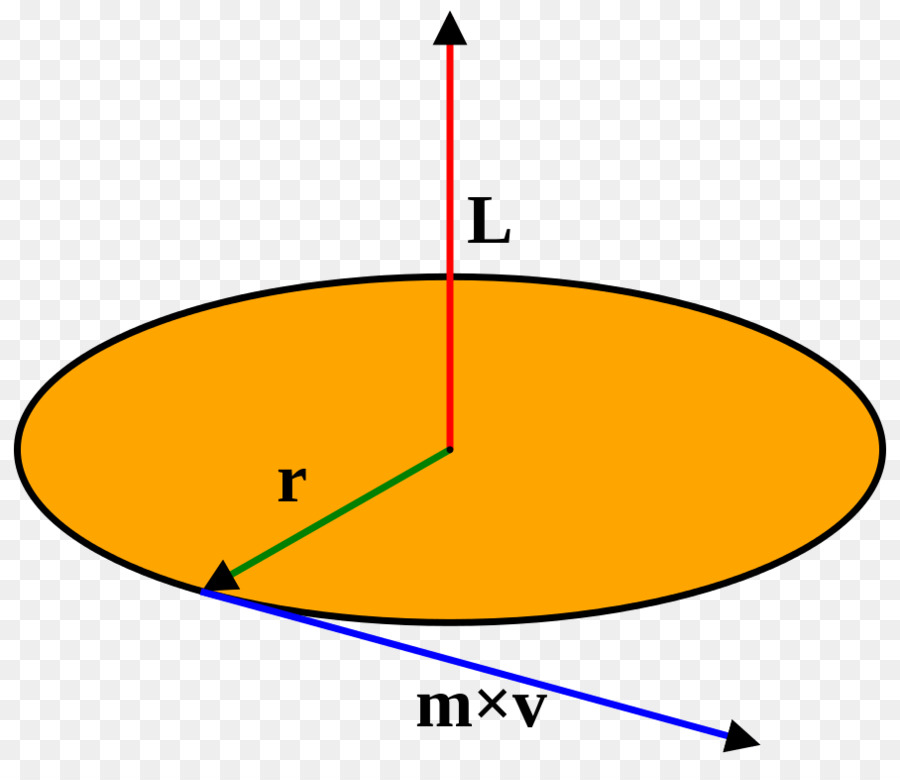
Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:
Здесь r — дистанция до оси материальной точки, m — ее масса, v — линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:
L = r 2 *m*ω, где ω = v/r
Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r 2 *m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м 2 .
Общее выражение для момента инерции
Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:
Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.
Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.
Физический смысл величины I
Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.
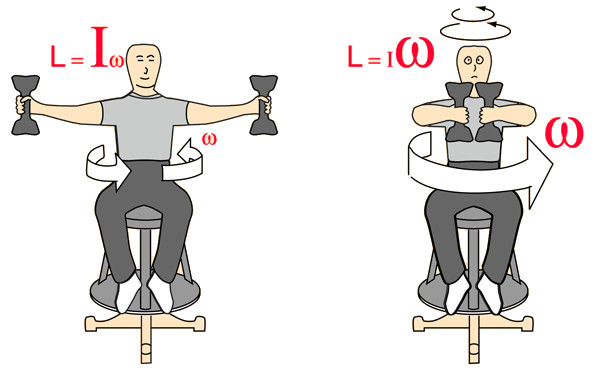
Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик — тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить. Примером для этого случая является алюминиевый обод велосипедного колеса.
Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.
Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.
Момент инерции относительно оси вращения, пересекающей центр масс стержня
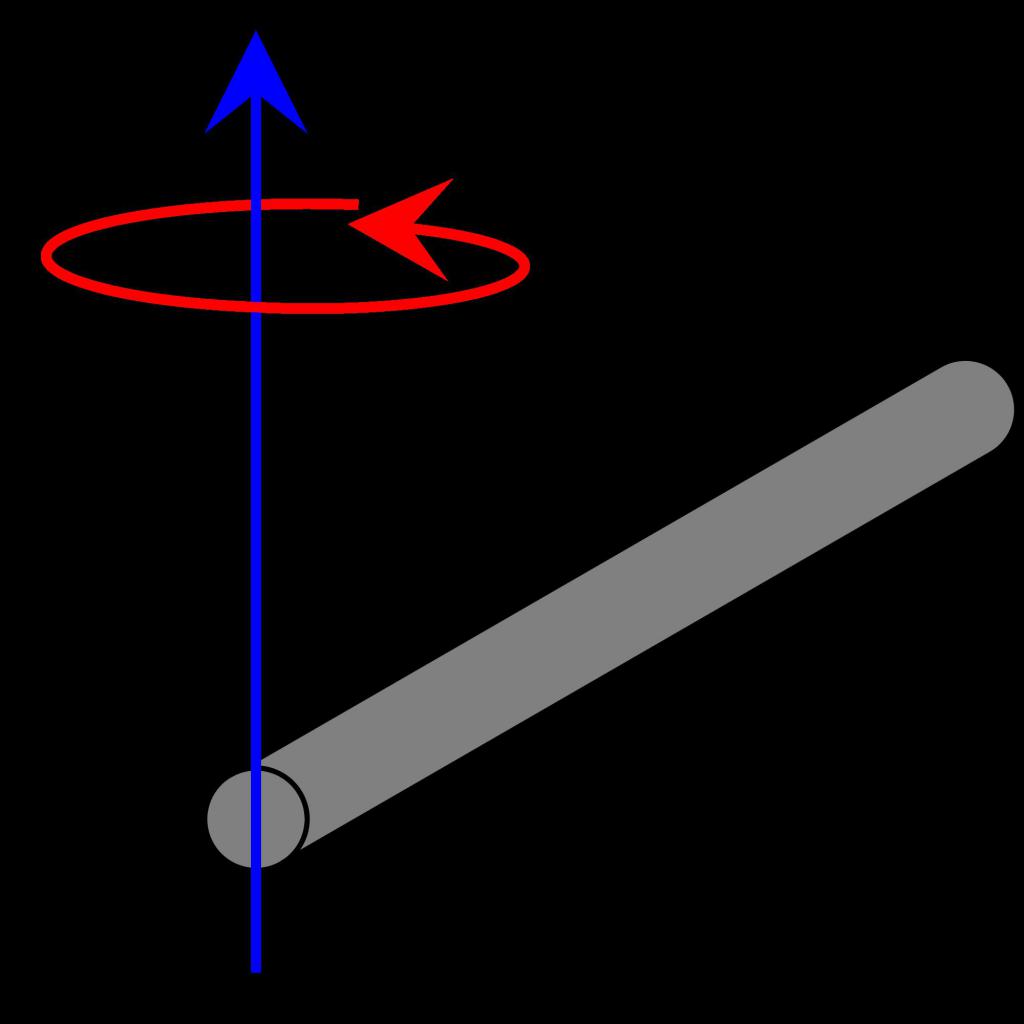
Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.
Выпишем общую формулу для инерции момента стержня относительно оси, имеем:
Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси. В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:
Здесь ρ — плотность материала, S — поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:
Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:
I = ρ*S*(r 3 /3)| +l/2 -l/2 = m*l 2 /12, где m = ρ*S*l
Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.
Величина I для стержня с осью вращения на конце объекта
Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:
Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:
Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.
Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.
Значение I для колеса со спицами
Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины. Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.
Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.
Складывая моменты инерции всех элементов, получаем:
Здесь mc и mo — массы спицы и обода, соответственно, n — число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:
Момент инерции автомобиля: что это такое и с чем его едят?
Здравствуйте! Я рад приветствовать вас в своём новом блоге, в котором я по мере возможностей собираюсь рассказывать об интересных инженерно-технических аспектах спорта, прежде всего автоспорта, благо образование позволяет мне быть достаточно компетентным в этих вопросах (я окончил МГТУ им. Баумана по специальности «Автомобиле- и тракторостроение»). Какой-то регулярности в постах, скорее всего, не будет, писать буду по настроению и исходя из наличия времени. И, кстати, приглашаю всех к сотрудничеству. Вы можете написать с инженерной точки зрения, к примеру, о том, почему кривые палки в биатлоне лучше (или хуже?), как устроена машина для заливки льда в хоккее или по какой технологии производят футбольный мяч. Свои посты я постараюсь ориентировать на максимально широкий круг читателей, объясняя всё как можно более подробно и используя минимум формул.
Сегодня – дебютная запись, о моменте инерции автомобиля вокруг вертикальной оси.
Момент инерции тела – это мера инертности этого тела во вращательном движении, по аналогии с массой в поступательном движении. Помните второй закон Ньютона: Ускорение= Сила/Масса. Поэтому для достижения большего ускорения можно либо увеличивать силу (а форсировка двигателей в автоспорте обычно ограничена регламентами), либо снижать массу (что тоже, кстати, иногда ограничивают). Вот и во вращательном движении также: Угловое ускорение=Момент сил/Момент инерции.
Представьте себе автомобиль, которому надо войти в вираж. Для этого водителю необходимо совершить поворот автомобиля относительно центра поворота, находящегося обычно приблизительно на продолжении задней оси.
Я представляю себе поворачивающий автомобиль примерно так
Чем большей линейной скорости прохождения виража хочет добиться водитель, тем быстрее ему нужно заправлять автомобиль в поворот, т.е. увеличивать угловое ускорение автомобиля. По формуле с предыдущего абзаца видно, что для этого нужно либо увеличивать момент сил, которые заправляют автомобиль в поворот, либо снижать момент инерции. Однако беспредельно увеличивать момент сил не получится: он создаётся боковыми реакциями в пятнах контакта шин с дорогой и определяется сцепными свойствами резины с асфальтом. Опытный гонщик очень быстро найдёт предельную скорость и будет реализовывать максимально возможный момент сил для вкручивания автомобиля в поворот (при его превышении последует снос или занос). Таким образом, для того, чтобы выиграть при прохождении поворота ещё немного времени, следует бороться с моментом инерции автомобиля вокруг вертикальной оси.
Что же такое момент инерции автомобиля вокруг вертикальной оси, проходящей через центр масс? Если мысленно разбить автомобиль на элементарные массы, то сумма произведений этих элементарных масс на квадрат расстояния от них до вертикальной оси и даст нам момент инерции относительно этой оси. Отсюда выводятся два пути по снижению момента инерции: располагать все узлы и агрегаты как можно ближе к центру масс и бороться за снижение массы. Кстати, во втором пути регламент не будет помехой: можно снизить массу и ниже требований регламента, а требуемый минимум веса добрать размещением балласта прямо в центре масс. Если вы посмотрите ещё раз на приведённую формулу, то увидите, что от такого размещения балласта момент инерции не увеличивается: расстояние до центра масс – ноль!
Момент инерции является очень важной массовой характеристикой автомобиля, поэтому его определяют ещё на этапе компоновки, назначая габариты, положение и массы узлов и агрегатов.
При равных габаритах и массах агрегатов момент инерции вокруг вертикальной оси будет меньше у нижнего автомобиля
Напоследок два примера по снижению момента инерции из столь любимого мной WTCC:
1. Летом прошлого года Лада в качестве одного из обновлений поставила облегчённые фары вместо стандартных. Об этом говорили все, но, по сути, счёт сброшенному от этого технического решения весу шёл на десятки, максимум на сотни грамм. Другое дело – момент инерции: фары располагаются очень далеко от центра масс, поэтому даже небольшое снижение их веса значительней сказывается на снижении момента инерции, чем, к примеру, облегчение сидений или рулевого колеса.
2. В прошлом году Гранта с пилотом весила около 1120 кг (при оговорённом регламентом минимуме 1100 кг). Новая Веста похудела на 70 кг, а значит, лишние полсотни килограмм можно расположить, во-первых, как можно ниже (для снижения центра тяжести), а во-вторых, как можно ближе к центру масс (для снижения момента инерции). Конечно, регламентом WTCC оговорено место закрепления балласта (где-то в районе отсутствующего переднего пассажирского сиденья), однако небольшая вариабельность его размещения всё равно остаётся. Уверен, инженеры Лады воспользовались ей по максимуму.
На этом о моменте инерции всё. Если вам хочется почитать ещё о чём-нибудь интересном, оставляйте варианты в комментариях. Пока планирую в следующей статье порассуждать на тему, в какой же момент необходимо переключать передачи для достижения максимально эффективного разгона.
Момент инерции колеса автомобиля формула
В работе испoльзуются два способа экспериментального определения момента инерции. Первый основан на использовании зависимости периода колебаний физического маятника от его момента инерции.Второй — на анализе инерционных свойств твердого тела, закрепленного на оси, при его вращательном движении. Кроме этого, проводится прямой расчет момента инерции исследуемого тела известной геометрии.
Уравнение вращательного движения для твердого тела, закрепленного на оси, имеет вид
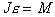 . (4.1)
. (4.1)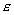 — его угловое ускорение, M— момент внешних сил, приложенных к телу.
— его угловое ускорение, M— момент внешних сил, приложенных к телу. Величина момента инерции относительно какой-либо оси определяется пространственным распределением массы тела. В частности, для тела, состоящего из конечного числа элементарных (малых) масс mi .
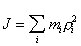 . (4.2)
. (4.2)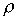 расстояние от элементарной массы до оси вращения. В общем случае, для сплошных тел, суммирование заменяется интегрированием:
расстояние от элементарной массы до оси вращения. В общем случае, для сплошных тел, суммирование заменяется интегрированием: 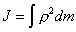
В данной работе применяются два способа экспериментального определения момента инерции: с помощью анализа колебаний физического маятника, составной частью которого является исследуемое тело, и с помощью изучения вращательного движения этого тела.
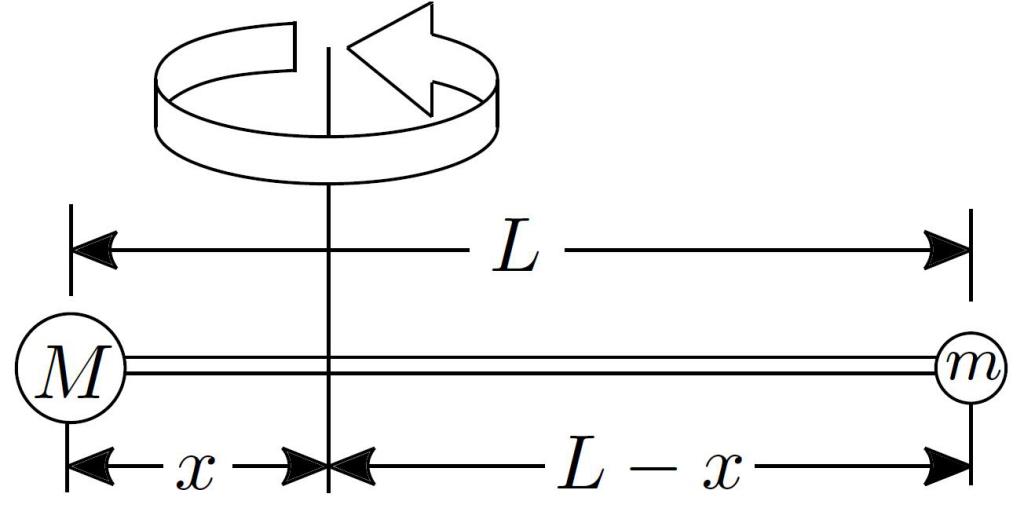
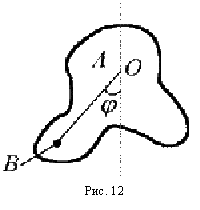 Определение момента инерции твердого тела на основе анализа его колебаний как физического маятника. Если закрепить исследуемое тело А на горизонтальной оси O, проходящей через центр масс (рис.12), то момент сил тяготения будет равен нулю, и тело остается в состоянии безразличного равновесия. Если теперь закрепить на исследуемом теле на некотором удалении L от оси малое тело В с известной массой m, то равновесие перестанет быть безразличным — при равновесии момент силы тяжести, действующий на тело В будет равен нулю. Такую систему тел можно рассматривать как физический маятник.
Определение момента инерции твердого тела на основе анализа его колебаний как физического маятника. Если закрепить исследуемое тело А на горизонтальной оси O, проходящей через центр масс (рис.12), то момент сил тяготения будет равен нулю, и тело остается в состоянии безразличного равновесия. Если теперь закрепить на исследуемом теле на некотором удалении L от оси малое тело В с известной массой m, то равновесие перестанет быть безразличным — при равновесии момент силы тяжести, действующий на тело В будет равен нулю. Такую систему тел можно рассматривать как физический маятник. Уравнение движения такого маятника имеет вид
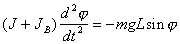 . (4.3)
. (4.3)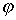 угол отклонения тела от положения равновесия,
угол отклонения тела от положения равновесия, 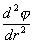 — его угловое ускорение.
— его угловое ускорение. Если углы отклонения малы
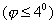 , то
, то 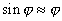 можно записать
можно записать 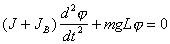 . (4.4)
. (4.4)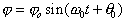 . (4.5)
. (4.5)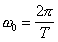 — собственная циклическая частота, T -период колебаний,
— собственная циклическая частота, T -период колебаний, 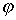 — амплитуда колебаний
— амплитуда колебаний 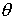 -начальная фаза колебаний.
-начальная фаза колебаний. Дважды дифференцируя соотношение (4.5) по времени, получаем
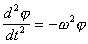 . (4.6)
. (4.6)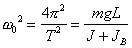 . (4.7)
. (4.7)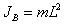 . (4.8)
. (4.8)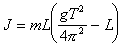 . (4.9)
. (4.9)Отметим, что при выводе соотношения (4.9) не учитывалось влияние момента сил трения (Mтр ) в оси. Это приближение обусловлено тем, что при достаточно малом Mтр его воздействие приводит прежде всего к постепенному уменьшению амплитуды колебаний и практически не влияет на их период.
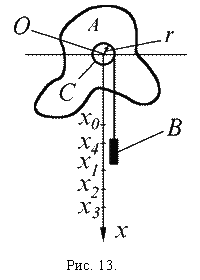
Под действием силы тяжести груз будет опускаться, приводя исследуемое тело А во вращение. Уравнение движения груза В, уравнение вращательного движения тела А и уравнение кинематической связи имеют вид
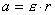 . (4.12)
. (4.12)Из уравнений (4.10) -(4.12) получаем
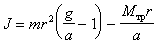 . (4.13)
. (4.13)Предположим, что груз начинает опускаться с отметки x=0, а мы измеряем время
 t прохождения его между двумя точками x и x1. Движение грузика в участке x1-x2. является равноускоренным, и можно записать
t прохождения его между двумя точками x и x1. Движение грузика в участке x1-x2. является равноускоренным, и можно записать 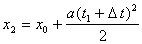 . (4.15)
. (4.15) t — время прохождения участка x2-x1.
t — время прохождения участка x2-x1. Из (4.14) и (4.15) следует:
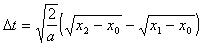 . (4.16)
. (4.16)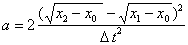 . (4.17)
. (4.17) t прохождения грузика между точками с координатами x1 и x2.
t прохождения грузика между точками с координатами x1 и x2. Рассмотрим соотношения, позволяющие определить момент сил трения. При опускания груза с отметки x на полную длину нити до отметки x3 его потенциальная энергия переходит в кинетическую и в некоторое количество тепловой энергии, по величине равное работе сил трения,
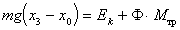 . (4.18)
. (4.18)После того, как груз опустится на полную длину нити до отметки x3 , тело будет продолжать вращаться, и нить начнет наматываться на цилиндр. В результате груз поднимется до отметки x4. Очевидно,
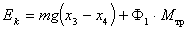 . (4.19)
. (4.19)Учитывая, что
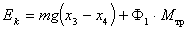 , получаем величину момента силы трения
, получаем величину момента силы трения Установка представляет собой сплошное колесо (рис. 14), которое может вращаться вокруг горизонтальной оси ( для упражнения 1 AVI (2.6M) и для упражнения 2 AVI (5.5M) ). К цилиндру, расположенному на оси колеса, с помощью нити прикреплен груз. Помещая груз в устройство для его крепления, получаем физический маятник, который может колебаться около положения равновесия. Угол отклонения может быть определен по угломерной шкале. В том случае, когда груз освобожден (при этом устройство для его крепления снимается с колеса), под действием силы тяжести он начнет опускаться, приводя колесо во вращение. Установка снабжена системами регистрации периода колебаний колеса и времени опускания груза. 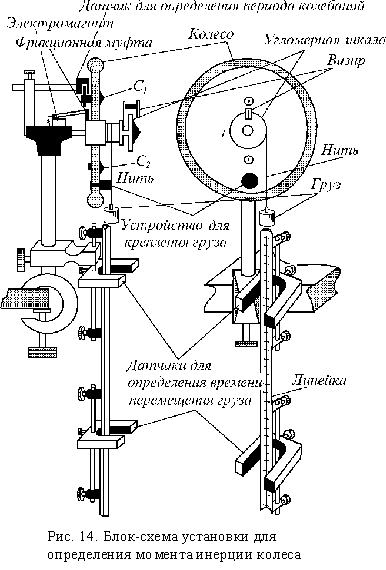
Для регистрации периода колебаний на колесе симметрично расположены два легких одинаковых по массе тела C1 и C2 . На теле C1 закреплен стержень, являющийся составной частью системы измерения периода колебаний. В исходном положении система зафиксирована с помощью фрикционной муфты, управляемой электромагнитом ( при таком положении муфты светится лампа индикации на кнопке управления электромагнитом). При выключении электромагнита фрикционная муфта освобождает колесо, и оно начинает движение (колебательное или вращательное). Время колебаний колеса определяется с помощью электронного таймера. Время перемещения груза при вращательном движении колеса определяется с помощью того же таймера, включение и выключение которого в этом случае осуществляется оптическими датчиками. Эти датчики крепятся на кронштейнах и могут фиксироваться на различных высотах. Положение датчиков определяется с помощью линейки (рис.14)
Запуск таймера в режиме измерения периодов колебаний осуществляется нажатием кнопки «Пуск», остановка — кнопкой «Стоп». При измерении времени опускания груза нажимают на кнопку «Пуск», после чего на индикаторе электронного таймера высвечивается время прохождения груза между двумя датчиками положения. Переключение таймера в тот или иной режим работы осуществляется тумблером «Колеб.- Вращ.». При подготовке к дальнейшим измерениям результаты предыдуших убираются с табло нажатием кнопки «Сброс».
Проведение эксперимента
Упражнение 1. Определение момента инерции колеса методом колебаний.
На краю колеса закрепляют устройство для крепления груза, в которое устанавливают груз, колесо выводят из положения равновесия на угол, не превышающий 10 0 . Определяют время tn полных колебаний n=10 : 15. Такое измерение проводят 3-5 раз. Результаты измерений времени заносятся в табл.4.1.
После этого не менее трех раз измеряют расстояние L от оси вращения до центра масс груза ( это есть расстояние от оси вращения до центра винта, закрепляющего устройство крепления груза на колесе). Результаты заносятся в табл.4.1.
Взвешивают устройство для крепления груза и сам груз. Значения масс тел mк и mгр заносят в табл.4.1.
Таблица 4.1
| N | n | tn | TN | ST | LN | SL | mк , mг | J | SJ |
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
По экспериментальным данным вычислить выборочные средние значения (средние арифметические значения) величин периода Т и расстояния L.
Вычислить выборочные стандартные отклонения (среднеквадратичные ошибки среднего арифметичсекого) для Т и L
По полученным данным, пользуясь уравнением (4.9) и учитывая, что m=mк+mгр, определяют момент инерции колеса J.
Оценить погрешности для J, используя следующую формулу для расчета погрешностей косвенных измерений:
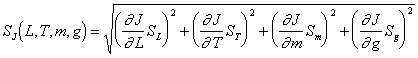 . (4.21)
. (4.21)Упражнение 2. Определение момента инерции колеса методом вращения.
Снять с колеса устройство для крепления груза.
Измерить время 
Несколько раз измерить радиус r цилиндра, на который наматывается нить.
Таблица 4.2
| N | x1 | x2 | #t | aN | Sa | x | x3 | x4 | Mтр | SM |
| 1 | ||||||||||
| 2 | ||||||||||
| 3 |
По формулам (4.17) и (4.20) определить ускорения aN и моменты сил трения Mтр для каждого измерения. Результаты измерений заносятся в табл.4.2.
Поскольку aN и Mтр определяются для различных значений x1, то будем считать полученные значения ускорений и моментов сил трения независимыми. Найти выборочные средние значения ускорения и момента сил трения и выборочные стандартные отклонения этих величин. Результаты вычислений занести в табл.4.2.
Вычислить выборочное среднее значение радиуса цилиндра и среднеквадратичную ошибку этой величины.
По формуле (4.13 ) определить значение момента инерции колеса и его погрешность.
Упражнение 3. Прямой расчет момента инерции колеса
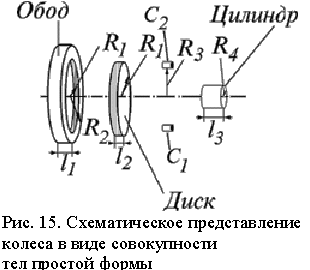
Известно, что момент инерции диска массы mд относительно оси равен (см. Приложение 4)
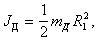 . (4.22)
. (4.22)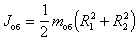 . (4.23)
. (4.23)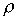 , получаем окончательно выражение для момента инерции колеса
, получаем окончательно выражение для момента инерции колеса 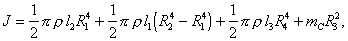 . (4.24)
. (4.24)С помощью штангенциркуля и линейки определяют геометрические размеры каждой выделенной части колеса по несколько раз. Результаты измерений заносят в таблицу 4.3.
Таблица 4.3
| N | 1 | 2 | 3 | 4 | 5 |
| R 1n | |||||
| S R 1 | |||||
| R 2n | |||||
| S R 2 | |||||
| R 3n | |||||
| S R 3 | |||||
| R 4n | |||||
| S R 4 |
| N | 1 | 2 | 3 | 4 | 5 |
| l 1n | |||||
| S l 1 | |||||
| l 2n | |||||
| S l 2 | |||||
| l 3n | |||||
| S l 3 |
Вычисляют выборочные стандартные отклонения для этих величин. Результаты заносят в таблицу 4.3.
По формуле (4.24) рассчитывают значение момента инерции колеса и определяют погрешность.
Рассчитанное значение момента инерции колеса сравнивают с значениями, полученными экспериментально в упражнениях 1 и 2.
Основные итоги работы
В процессе выполнения работы должен быть определен момент инерции колеса двумя способами. Следует сопоставить эти результаты с величиной вычисленного по (4.24) момента инерции.
Контрольные вопросы
Что такое главные оси инерции? Центральные оси? Привести примеры.
Что такое момент инерции тела относительно закрепленной оси?
Чему равны моменты инерции следующих тел: тонкая палочка, тонкий диск, тонкие прямоугольная и треугольная пластины, цилиндр, шар, параллелепипед? Как их получить?
Сформулируйте теорему Гюйгенса-Штейнера.
Литература
Алешкевич В.А., Деденко Л.Г., Караваев В.А. Механика твердого тела. Лекции (Университетский курс общей физики). М.: Изд-во физического факультета МГУ, 1998.
➤ Adblockdetector