Открытый урок физики по теме «Криволинейное движение». 9-й класс
Класс: 9
Презентация к уроку
Загрузить презентацию (629,3 кБ)
Цели урока: дать школьникам представление о криволинейном движении, частоте, угловом перемещении, угловой скорости, периоде. Познакомить с формулами для нахождения этих величин и единицами измерения. (Слайды 1 и 2)
Ззадачи:
Образовательные: дать учащимся представление о криволинейном движении его траектории, величинах его характеризующих, единицах измерения этих величин и формулах для вычисления.
Развивающие:продолжать формирование умений применять теоретические знания для решения практических задач, развивать интерес к предмету и логическое мышление.
Воспитательные: продолжать развивать кругозор учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.
Оборудование: наклонный жёлоб, шарик, шарик на нити, игрушечный автомобиль, юла, модель часов со стрелками, мультимедийный проектор, презентация.
1. Актуализация знаний
Учитель.
– Какие виды движения вы знаете?
– Чем отличаются прямолинейные и криволинейные движения?
– В какой системе отсчёта можно говорить об этих видах движения?
– Сравните траекторию и путь для прямолинейного и криволинейного движений. (Слайды 3, 4).
2. Объяснение нового материала
Учитель. Демонстрирую: падение шарика по вертикали, его скатывание по желобу, вращение шарика на нити, перемещение игрушечного автомобиля по столу, падение теннисного мячика брошенного под углом к горизонту.
Учитель. Чем отличаются траектории движения предложенных тел? (Ответы учащихся)
Попробуйте сами дать определения криволинейного и прямолинейного движений. (Запись в тетрадях):
– прямолинейное движение – движение по прямой траектории, причём направление векторов силы и скорости совпадают; (слайд 7)
– криволинейное движение – движение по непрямой траектории.
Рассмотреть два примера криволинейного движения: по ломаной линии и по кривой (Зарисовать, слайды 5, 6).
Учитель. Чем отличаются эти траектории?
Ученик. В первом случае траекторию можно разбить на прямолинейные участки и рассмотреть каждый участок отдельно. Во втором случае можно разбить кривую на дуги окружностей и прямолинейные участки Т.о. это движение можно рассматривать как последовательность движений, происходящих по дугам окружностей различного радиуса (Слайд 8)
Учитель. Приведите примеры прямолинейного и криволинейного движения, с которыми вы встречались в жизни.
3. Сообщение ученика. В природе и технике очень часто встречаются движения, траектории которых представляют собой не прямые, а кривые линии. Это криволинейное движение. По криволинейным траекториям движутся в космическом пространстве планеты и искусственные спутники Земли, а на Земле всевозможные средства транспорта, части машин и механизмов, воды рек, воздух атмосферы и т.д.
Если прижать к вращающемуся точильному камню конец стального прутика, то раскаленные частицы, отрывающиеся от камня, будут видны в виде искр. Эти частицы летят с той скоростью, которой они обладали в момент отрыва от камня. Хорошо видно, что направление движения искр совпадает с касательной к окружности в той точке, где пруток касается камня. По касательной движутся брызги от колес буксующего автомобиля. (Слайд 9)
Учитель. Таким образом, мгновенная скорость тела в разных точках криволинейной траектории имеет различное направление, причём, обратите внимание: вектора скорости и силы, действующей на тело, направлены по пересекающимся прямым. (Слайды 10 и 11).
По модулю же скорость может быть всюду одинакова или изменяться от точки к точке.
Но даже если модуль скорости не изменяется, ее нельзя считать постоянной. Скорость – векторная величина. Для векторной величины модуль и направление одинаково важны. А раз меняется скорость, значит есть ускорение. Поэтому криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянная. (Слайд 12).
Ускорение тела, равномерно движущегося по окружности, в любой точке центростремительное, т.е. направлено по радиусу окружности к ее центру. В любой точке вектор ускорения перпендикулярен вектору скорости. (Нарисовать)
Модуль центростремительного ускорения: ац = V 2 /R (написать формулу), где V – линейная скорость тела, а R – радиус окружности. (Слайды 12, 13)
Учитель. Движение по окружности часто характеризуют не скоростью движения, а промежутком времени, за который тело совершает один полный оборот. Эта величина называется периодом обращения и обозначается буквой Т. (Записать определение периода). Найдем связь между периодом обращения Т и модулем скорости при равномерном движении по окружности радиуса R. Т.к. V = S/t = 2
Сообщение ученика. Период – это величина, которая достаточно часто встречается в природе и технике. Так, мы знаем. Что Земля вращается вокруг своей оси и средний период вращения равен 24 часам. Полный оборот Земли вокруг Солнца происходит примерно за 365,26 суток. Рабочие колеса гидротурбин делают один полный оборот за время, равное 1 секунде. А винт вертолета имеет период обращения от 0,15 до 0,3 секунды. Период кровообращения у человека равен примерно 21-22 секундам.
Учитель. Движение тела по окружности можно охарактеризовать еще одной величиной – числом оборотов в единицу времени. Ее называют частотой обращения: ν = 1/Т. Единицей измерения частоты: с –1 = Гц. (Записать определение, единицу и формулу) (слайд 14)
Сообщение ученика. Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля, вылетающая из автомата Калашникова, вращается с частотой 3000 об/с.
Для измерения частоты существуют приборы, так называемые круги для измерения частоты, основанные на оптических иллюзиях. На таком круге нанесены черные полоски и стоят частоты. При вращении такого круга черные полоски образуют круг при соответствующей этому кругу частоте. Также для измерения частоты используются тахометры. (Слайд 15)
(Дополнительные характеристики слайды 16, 17)
4. Закрепления материала (слайд18)
Учитель. На этом уроке мы познакомились с описанием криволинейного движения, с новыми понятиями и величинами. Ответьте мне на следующие вопросы:
– Как можно описать криволинейное движение?
– Что называется угловым перемещением? В каких единицах измеряется?
– Что называется периодом и частотой? Как связаны между собой эти величины? В каких единицах измеряются? Как их можно определить?
– Что называется угловой скоростью? В каких единицах она измеряется? Как можно её рассчитать?
(Если остаётся время, можно выполнить экспериментальное задание по определению периода и частоты вращения тела, подвешенного на нити.)
5. Экспериментальная работа: измерение периода, частоты тела, подвешенного на нити и вращающегося в горизонтальной плоскости. Для этого на каждую парту приготовить набор принадлежностей: нить, тело (бусинка или пуговица), секундомер; инструкцию по выполнению работы: тело вращать равномерно, (для удобства работу можно выполнять вдвоём) и измерить время 10 (вспомнить определение полного оборота). (После выполнения работы обсудить полученные результаты). (Cлайд 19)
6. Контроль и самопроверка
Учитель. Следующее задание на проверку, как вы усвоили новый материал. У каждого из вас на столах лежат тесты и две таблицы, в которые вы должны внести букву ответа. Одну из них вы подпишите и сдадите на проверку. (Тест 1 выполняет 1 вариант, тест 2 – второй вариант)
Тест 1 (слайд 20)
1. Примером криволинейного движения являются.
а) падение камня;
б) поворот машины на право;
в) бег спринтера на 100 – метровке.
2. Минутная стрелка часов делает один полный оборот. Чему равен период обращения?
3. Колесо велосипеда делает один оборот за 4 с. Определите частоту вращения.
4. Винт моторной лодки делает 25 оборотов за 1 с. Чем, равна угловая скорость винта?
а) 25 рад/с; б)
/25 рад/с; в) 50
рад/с.
5. Определите частоту вращения сверла электрической дрели, если его угловая скорость равна 400 
а)800 1/с; б) 400
1/с; в) 200 1/с.
Тест 2 (слайд 20)
1. Примером криволинейного движения является…
а) движение лифта;
б) прыжок лыжника с трамплина;
в) падение шишки с нижней ветки ели в безветренную погоду.
2. Секундная стрелка часов делает один полный оборот. Чему равна её частота обращения?
3. Колесо машины делает 20 оборотов за10 с. Определите период обращения колеса?
4. Ротор мощной паровой турбины делает 50 оборотов за 1 с. Вычислите угловую скорость.
а) 50
рад/с; б)
/50 рад/с; в) 10
рад/с.
5. Определите период обращения звёздочки велосипеда, если угловая скорость равна.
Ответы на тест 1: б; в; а; в; в
Ответы на тест 2: б; а; в; в; б (слайд 21)
7. Подведение итогов
8. Домашнее задание: § 18, 19, вопросы к §§, упр.17, (устно) (слайд 21)
Учебники
Журнал «Квант»
Общие
Уровень А
1. Колесо совершает за одну минуту:
б) 1500 оборотов.
Определите его период.
2. Период вращения лопастей ветряной мельницы равен 5 с. Определите число оборотов лопастей за 1 ч.
3. Определите частоту движения:
б) минутной, – стрелок механических часов.
Секундная стрелка часов совершает один оборот за 1 мин, минутная стрелка – один оборот за 1 ч.
4. Частота вращения воздушного винта самолета 25 Гц. За какое время винт совершает 3000 оборотов.
5. Период вращения Земли вокруг своей оси равен 1 сут. Определите частоту ее вращения.
6. Колесо совершило 15 полных оборотов. Определите его угловое перемещение.
7. Колесо радиуса 0,5 м прокатилось 100 м. Определите угловое перемещение колеса.
8. Определите угловую скорость вращения колеса, если за 60 с колесо поворачивается на 20π.
9. Угловая скорость барабана сепаратора 900 рад/с. Определите угловое перемещение барабана за 15 с.
10. Определите угловую скорость вала, вращающегося:
а) с периодом 10 с;
б) с частотой 30 Гц.
11. Маховик вращается с постоянной угловой скоростью 9 рад/с. Определите:
а) частоту его вращения;
б) период его вращения.
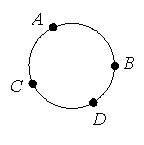
12. Укажите направление скорости в точках А, В, С, D (рис. 1), если круг вращается:
а) по часовой стрелке;
б) против часовой стрелки.
13. Колесо велосипеда имеет радиус 25 см. Определите линейную скорость точек обода колеса, если оно вращается с частотой 4 Гц.
14. Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.
15. Скорость точек экватора Солнца при его вращении вокруг своей оси равна 2,0 км/с. Найдите период вращения Солнца вокруг своей оси, если радиус Солнца 6,96∙10 8 м.
16. Тело движется по окружности радиусом 3 м со скоростью 12π м/с. Чему равна частота обращения?
17. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость тела, если известно, что его угловая скорость равна π рад/с.
18. Спортсмен бежит равномерно по окружности радиусом 100 м со скоростью 10 м/с. Определите его угловую скорость.
19. Укажите направление ускорения в точках A, B, C, D при движении по окружности (рис. 2).
20. Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?
21. Каков радиус кривизны закругления дороги, если по ней автомобиль движется с центростремительным ускорением 1 м/с 2 при скорости 10 м/с?
22. С какой скоростью велосипедист проходит закругление велотрека радиусом 50 м, если он имеет центростремительное ускорение 2 м/с 2 ?
23. Шкив вращается с угловой скоростью 50 рад/с. Определите центростремительное ускорение точек находящихся на расстоянии 20 мм от оси вращения.
24. Земля вращается вокруг своей оси с центростремительным ускорением 0,034 м/с 2 . Определите угловую скорость вращения, если радиус Земли 6400 км.
Уровень B
1. Может ли тело двигаться по окружности без ускорения?
2. Первая в мире орбитальная космическая станция, образованная в результате стыковки космических кораблей «Союз-4» и «Союз-5» 16 января 1969 г., имела период вращения 88,85 мин и среднюю высоту над поверхностью Земли 230 км (считайте орбиту круговой). Найдите среднюю скорость движения станции. Радиус Земли принять равным 6400 км.
3. Искусственный спутник Земли (ИСЗ) движется по круговой орбите со скоростью 8,0 км/с с периодом вращения 96 мин. Определите высоту полета спутника над поверхностью Земли. Радиус Земли принять равным 6400 км.
4. Какова линейная скорость точек Земной поверхности на широте Санкт-Петербурга (60°) при суточном вращении Земли? Радиус Земли принять равным 6400 км.
5. Допустимо ли насадить точильный круг на вал двигателя, делающего 2850 оборотов в минуту, если на круге имеется штамп завода «35 м/с, Ø 250 мм»?
6. Скорость поезда 72 км/ч. Сколько оборотов в минуту делают колеса локомотива, радиус которых 1,2 м?
7. Какова угловая скорость вращения колеса ветродвигателя, если за 2 мин колесо сделало 50 оборотов?
8. За какое время колесо, имеющее угловую скорость 4π рад/с, сделает 100 оборотов?
9. Диск диаметром 50 см равномерно перекатывают на расстояние 2 м за 4 с. Какова угловая скорость вращения диска?
10. Тело движется по дуге окружности радиусом 50 м. Определите линейную скорость движения тела и пройденный им путь, если известно, что его угловое перемещение за 10 с равно 1,57 рад.
11. Как изменится линейная скорость вращения материальной точки по окружности, если угловую скорость точки увеличить в 2 раза, а расстояние от точки до оси вращения уменьшить в 4 раза?
12. Рабочее колесо турбины Красноярской ГЭС им. 50-летия СССР имеет диаметр 7,5 м и вращается с частотой 93,8 об/мин. Каково центростремительное ускорение концов лопаток турбины?
13. Ветряное колесо радиусом 2,0 м делает 40 оборотов в минуту. Найдите центростремительное ускорение концевых точек лопастей колеса.
14. Период вращения первого пилотируемого корабля-спутника «Восток» вокруг Земли был равен 90 мин. С каким ускорением двигался корабль, если его средняя высота над Землей 320 км? Радиус Земли принять равным 6400 км.
15. Угловая скорость вращения лопастей колеса ветродвигателя 6 рад/с. Найдите центростремительное ускорение концов лопастей, если линейная скорость концов лопастей 20 м/с.
16. Две материальные точки движутся по окружностям радиусами R1 = 10 см и R2 = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?
17. Две материальные точки движутся по окружностям радиусами R1 = 0,2 м и R2 = 0,4 м с одинаковыми периодами. Найдите отношение их центростремительных ускорений.