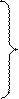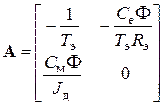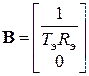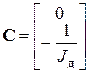Двигатель постоянного тока как объект управления



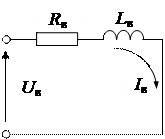
Электродвигатель постоянного тока (ДПТ) представляет собой объект управления, регулируемый, в общем случае, по цепям якоря и возбуждения [4]. Функциональная схема и схемы замещения электродвигателя приведены на рис. 4.2.
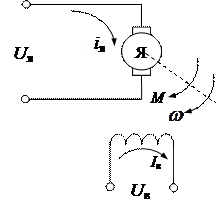 |

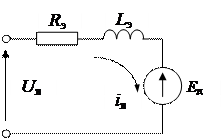
Рис. 4.2. Функциональная схема (а) и схемы замещения (б, в, г) электродвигателя постоянного тока
Применяя декомпозицию ДПТ, нетрудно заметить, что в его структуре имеются три основных подсистемы или цепи (см. рис. 4.2б, 4.2в, 4.2г):
— цепь якоря, питаемая регулируемым напряжением Uя; Rэ, Lэ – соответственно эквивалентное активное сопротивление и эквивалентная индуктивность якорной обмотки; Eд – э.д.с. электродвигателя; iя – ток якоря;
— цепь возбуждения, питаемая регулируемым напряжением Uв; Rв, Lв – соответственно эквивалентное активное сопротивление и эквивалентная индуктивность обмотки возбуждения; iв – ток возбуждения;
— электромеханическая цепь, обеспечивающая преобразование электромагнитной энергии в энергию вращения вала ротора; Jд – приведенный к валу двигателя момент инерции электродвигателя и вращаемого механизма; M, Mc – соответственно электромагнитный момент электродвигателя и момент сопротивления на его валу; 
Приведем описание ДПТ в различных формах, что позволит при необходимости легко установить взаимосвязь математических моделей.
Для описания динамических моделей электрических цепей электродвигателя (см. рис. 4.2) воспользуемся законами Кирхгофа, а для описания механической цепи – 2-м законом Ньютона. Тогда получим систему дифференциальных уравнений:
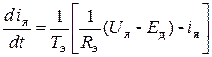
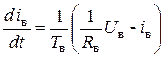
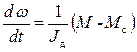
где 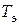
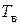
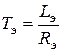
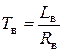
Электромагнитные цепи двигателя взаимосвязаны. При подаче напряжения 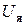
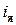
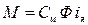
где 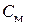
Электромагнитные и механическая цепь также взаимосвязаны, т.к. ток, протекающий по обмотке возбуждения, создает магнитный поток Ф, пронизывающий обмотку якоря и наводящий в ней э.д.с. вращения,
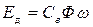
где 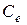
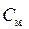
Анализируя выражения (4.24), (4.25), заметим, что произведение переменных приводит к нелинейности математической модели электродвигателя, регулируемого одновременно по цепям якоря и возбуждения. Кроме того, при регулировании напряжения возбуждения двигателя проявляется нелинейный характер изменения потока Ф в функции тока возбуждения iв (намагничивающей силы F = wв iв, где wв – число витков обмотки возбуждения). Кривая намагничивания ДПТ соответствует нелинейному звену типа «насыщение» (рис. 4.3).
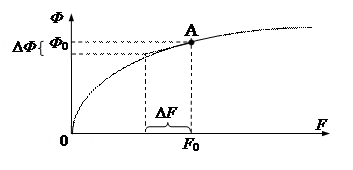 |
Рис. 4.3. Кривая насыщения магнитной цепи ДПТ
Рабочая точка А с координатами <F, Ф> на кривой насыщения соответствует некоторому, например номинальному режиму работы ДПТ.
ДПТ как нелинейный ОУ, регулируемый по цепям якоря и возбуждения, в соответствие с выражениями (4.23)…(4.25) и рис. 4.3 может быть представлен в виде структурной схемы (рис. 4.4)
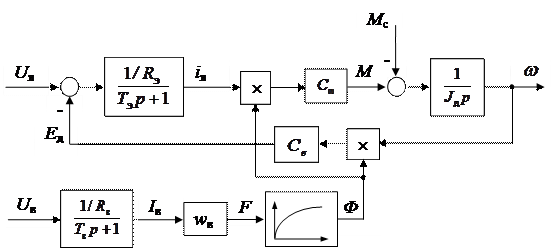 |
Рис. 4.4. Структурная схема ДПТ, регулируемого по цепям якоря
и возбуждения, как нелинейного объекта управления
Пусть электродвигатель регулируется только по цепи якоря (напряжение возбуждения 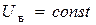
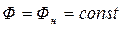
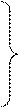
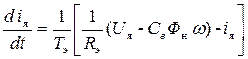
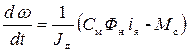
Математическая модель в виде (4.26) описывает ДПТ как линейный объект 2-го порядка.
Для перехода от дифференциальных уравнений (4.26) к операторным уравнениям произведем замену 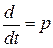
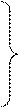
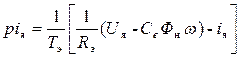
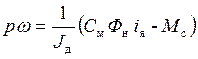
По операторным уравнениям (4.27) составим структурную схему электродвигателя, приведенную на рис. 4.4.
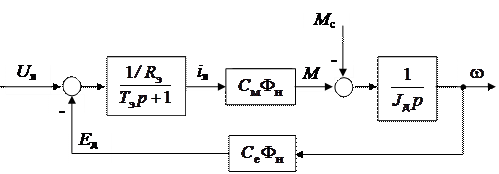 |
Рис. 4.5. Структурная схема ДПТ, регулируемого по цепи якоря
Как видим, структурная схема ДПТ, регулируемого по цепи якоря, содержит 4 типовых линейных динамических звена: апериодическое, интегрирующее и 2 безынерционных звена, а также 2 суммирующих звена.

Пусть ДПТ регулируется одновременно по цепи якоря и возбуждения, причем изменения аддитивных (управляющих и возмущающих) воздействий незначительны или, по крайней мере, непрерывны. Тогда нелинейную модель ДПТ целесообразно линеаризовать в окрестности вектора рабочих траекторий и представить в виде линейной модели. В качестве рабочих траекторий примем уравнения M = Cм Ф i я0, Eд = Cе Ф ω, а все переменные ДПТ будем рассматривать в приращениях, т. е. в малой окрестности рабочих траекторий и обозначать через символ приращения ∆. Проведем также касательную линеаризацию кривой намагничивания, задавшись координатами <F, Ф> текущей рабочей точки и соответствующими приращениями 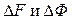
Тогда математическую модель ДПТ можно представить системой уравнений в приращениях
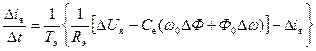
|
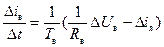
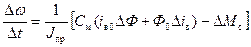
где 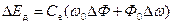
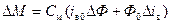
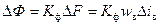
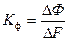
Структурная схема ДПТ, соответствующая уравнениям (4.28), приведена на рис. 4.6.
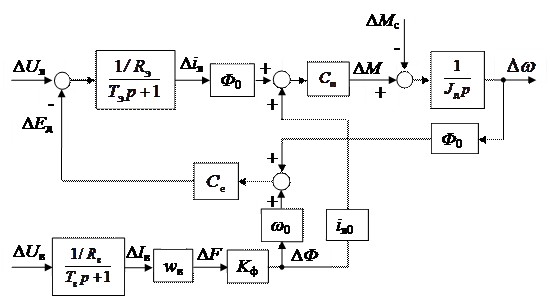 |
Рис. 4.6. Структурная схема ДПТ, регулируемого по цепям якоря
и возбуждения как линеаризованного объекта управления
Приведем векторно-матричное описание ДПТ как объекта регулирования по цепи якоря, т. е. будем полагать, что напряжение возбуждения 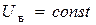
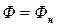
Воспользуемся векторно-матричной моделью линейных САУ в виде [4]
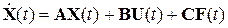
где 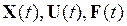
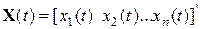
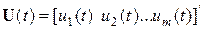
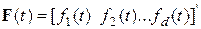

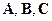
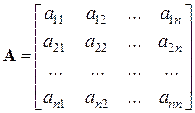
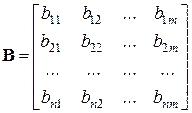
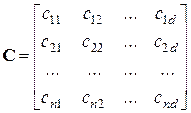
Зададимся векторами состояния, управления и возмущения в виде:
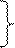
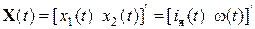
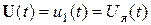
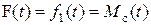
По уравнениям (4.29), (4.30) найдем матрицы состояния, управления и возмущения: